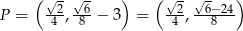/Szkoła średnia/Funkcje - wykresy/Styczna do wykresu/Wielomiany

Zadanie nr 9953660

Styczna do paraboli o równaniu 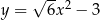√ -- 2 y = 6x − 3 w punkcie 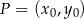P = (x 0,y 0) jest nachylona do osi 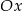Ox pod kątem 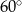6 0∘ . Oblicz współrzędne punktu P .

Wersja PDF

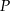Rozwiązanie

Liczymy pochodną danej funkcji

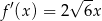
′ √ -- f (x) = 2 6x

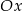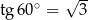Sprawdzamy w jakim punkcie tangens nachylenia stycznej do osi Ox jest równy √ -- tg60∘ = 3 .

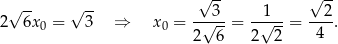
√ -- √ -- √ -- √ -- ---3- --1-- --2- 2 6x0 = 3 ⇒ x0 = √ --= √ --= 4 . 2 6 2 2

Stąd

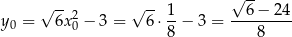
-- √ -- √ -- 1 √ 6− 2 4 y0 = 6x 20 − 3 = 6⋅ --− 3 = --------- 8 8

i 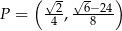( - - ) √-2 √-6−24 P = 4 , 8 .

PIC

 
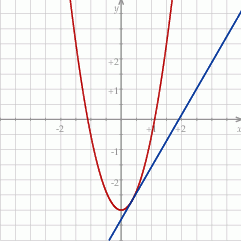
Odpowiedź: (√ - √ - ) ( √ - √- ) P = -42,-86− 3 = -42,-6−8-24-

Wersja PDF