/Szkoła średnia/Funkcje - wykresy/Styczna do wykresu/Funkcje wymierne

Zadanie nr 2616834

Dodaj do ulubionych
Dodaj do rozwiązanych

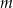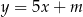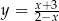Dla jakich wartości parametru m prosta y = 5x + m jest styczna do wykresu funkcji y = x2+−x3 ?

Rozwiązanie

Liczymy pochodną funkcji

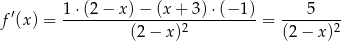
1 ⋅(2− x)− (x+ 3)⋅(− 1 ) 5 f ′(x ) = ----------------2----------= -------2- (2 − x) (2 − x)

Sprawdzamy teraz w jakich punktach współczynnik kierunkowy stycznej do wykresu funkcji 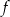f jest równy 5.

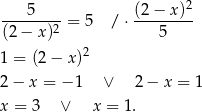
----5---- (2-−-x-)2 (2 − x)2 = 5 / ⋅ 5 2 1 = (2 − x) 2 − x = − 1 ∨ 2 − x = 1 x = 3 ∨ x = 1.

Styczne w tych punktach przechodzą odpowiednio przez punkty

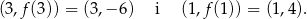
(3,f(3)) = (3,− 6) i (1,f(1)) = (1 ,4).

Pozostało wyznaczyć odpowiednie wartości 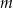m

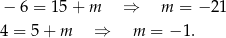
− 6 = 1 5+ m ⇒ m = − 2 1 4 = 5+ m ⇒ m = −1 .

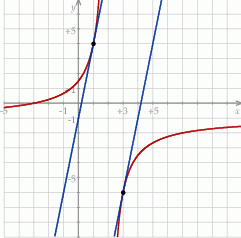
Na koniec rysunek dla ciekawskich.

PIC

 
Odpowiedź: 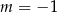m = − 1 lub m = − 21

Wersja PDF