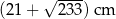Zadanie nr 3032388
Oblicz obwód trójkąta prostokątnego o polu powierzchni równym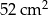 
, wiedząc, że długości jego przyprostokątnych różnią się o 5 cm.
Rozwiązanie
Szkicujemy trójkąt prostokątny.
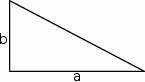
Jeżeli oznaczymy długości przyprostokątnych przez 
i 
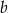to mamy układ równań
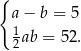
Podstawiając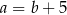 
z pierwszego równania do drugiego, otrzymujemy
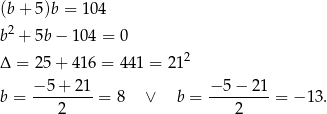
Ujemne rozwiązanie odrzucamy i mamy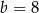 
oraz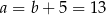 
. Długość przeciwprostokątnej wyliczamy z twierdzenia Pitagorasa
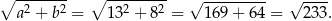
Obwód trójkąta jest więc równy
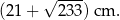
Odpowiedź: 
