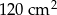Zadanie nr 3081442
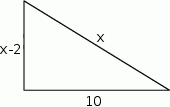
Oblicz sumę długości boków i pole trójkąta prostokątnego, w którym jedna z przyprostokątnych jest równa 10 cm, a druga jest o 2 cm krótsza od przeciwprostokątnej.
Rozwiązanie
Możemy sobie naszkicować taki trójkąt.
Na mocy twierdzenia Pitagorasa mamy równanie
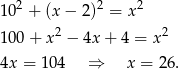
Zatem druga przyprostokątna ma długość 24 i suma boków jest równa
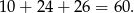
Pole trójkąta wynosi
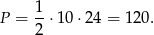
Odpowiedź: Suma długości boków: 60 cm, pole: