/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Oblicz długość...

Zadanie nr 3359022

Dodaj do ulubionych
Dodaj do rozwiązanych

Przeciwprostokątna trójkąta prostokątnego ma długość 26 cm, a jedna z przyprostokątnych jest o 14 cm dłuższa od drugiej. Oblicz obwód tego trójkąta.

Rozwiązanie

Jeżeli oznaczymy długość krótszej przyprostokątnej przez a , to druga przyprostokątna ma długość a + 14 .

PIC

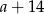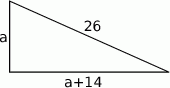
Zapisując twierdzenie Pitagorasa otrzymujemy równanie

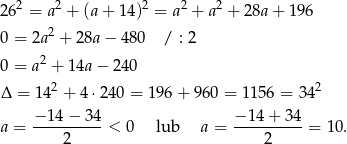
2 2 2 2 2 26 = a + (a+ 1 4) = a + a + 28a+ 196 0 = 2a2 + 28a− 480 / : 2 0 = a2 + 1 4a− 240 2 2 Δ = 14 + 4 ⋅240 = 1 96+ 960 = 11 56 = 34 −-14−--34- −-14-+-34- a = 2 < 0 lub a = 2 = 10.

Obwód trójkąta jest więc równy

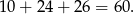
10+ 24 + 26 = 60 .

 
Odpowiedź: 60 cm

Wersja PDF