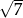/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Oblicz długość...

Zadanie nr 4885880

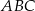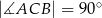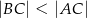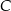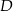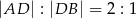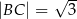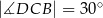W trójkącie prostokątnym ABC ( ∘ |∡ACB | = 90 , |BC | < |AC | ) poprowadzono prostą przechodzącą przez wierzchołek C trójkąta która przecina przeciwprostokątną w punkcie D , takim, że |AD | : |DB | = 2 : 1 . Oblicz długość przeciwprostokątnej jeśli |BC | = √ 3- i |∡DCB | = 3 0∘ .

Wersja PDF

Rozwiązanie

Zaczynamy naturalnie od rysunku.

PIC

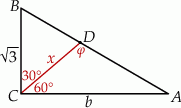
Sposób I

Z podanej informacji o stosunku w jakim punkt 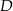D dzieli bok 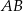AB wynika, że

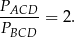
PACD--= 2. PBCD

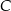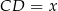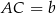(bo trójkąty te mają wspólną wysokość opuszczoną z wierzchołka C , a stosunek podstaw wynosi 2). Jeżeli oznaczymy CD = x i AC = b , to możemy te pola wyliczyć ze wzoru z sinusem.

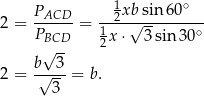
P 1 xbsin 60∘ 2 = --ACD- = --2--√--------- PBCD 12x⋅ 3sin 30∘ √ -- 2 = b√--3 = b. 3

Przeciwprostokątną liczymy z twierdzenia Pitagorasa

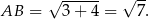
√ ------ √ -- AB = 3 + 4 = 7.

Sposób II

Tym razem skorzystamy z twierdzenia sinusów. Jeżeli oznaczymy 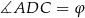∡ADC = φ to

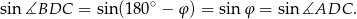
sin ∡BDC = sin (180∘ − φ) = sin φ = sin ∡ADC .

Piszemy teraz twierdzenia sinusów w trójkątach 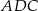ADC i BDC .

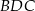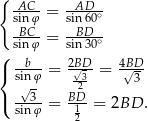
{ AC--= -AD-∘- siBnCφ sinB6D0 sinφ-= sin30∘- ( -b-- 2BD- 4BD- { sinφ = √3 = √3 √3 BD2 ( sinφ-= -1- = 2BD . 2

Podstawiamy teraz 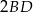2BD z drugiego równania do pierwszego i mamy

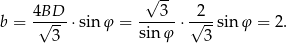
√ -- 4BD 3 2 b = √----⋅sinφ = ----- ⋅√---sinφ = 2. 3 sin φ 3

Stąd

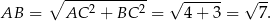
∘ ----2-----2- √ ------ √ -- AB = AC + BC = 4+ 3 = 7.

 
Odpowiedź: √ -- 7

Wersja PDF