/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Oblicz długość...

Zadanie nr 7122727

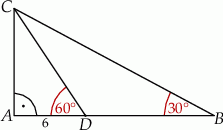
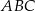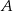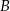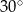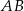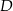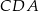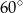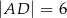W trójkącie ABC kąt przy wierzchołku A jest prosty, a kąt przy wierzchołku B ma miarę 30∘ . Na boku AB tego trójkąta obrano punkt D tak, że miara kąta CDA jest równa 60∘ oraz |AD | = 6 (zobacz rysunek). Oblicz |BD | .

PIC

Wersja PDF

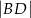Rozwiązanie

Sposób I

Trójkąt prostokątny 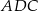ADC jest połówką trójkąta równobocznego o boku długości

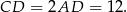
CD = 2AD = 12.

Ponadto

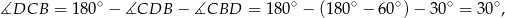
∘ ∘ ∘ ∘ ∘ ∘ ∡DCB = 180 − ∡CDB − ∡CBD = 180 − (180 − 60 )− 30 = 30 ,

więc trójkąt 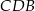CDB jest równoramienny i

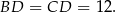
BD = CD = 12.

Sposób II

Z definicji funkcji trygonometrycznych mamy

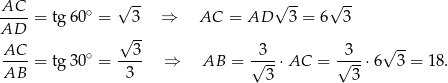
√ -- √ -- √ -- AC-- = tg 60∘ = 3 ⇒ AC = AD 3 = 6 3 AD √ -- AC 3 3 3 √ -- ----= tg 30∘ = ---- ⇒ AB = √---⋅AC = √--⋅ 6 3 = 18. AB 3 3 3

Mamy zatem

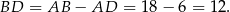
BD = AB − AD = 18− 6 = 12.

 
Odpowiedź: 12

Wersja PDF