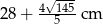/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Oblicz długość...

Zadanie nr 8763566

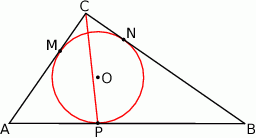
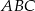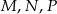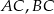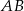W trójkąt prostokątny ABC wpisano okrąg. Punkty M ,N ,P są punktami styczności okręgu odpowiednio z bokami AC ,BC oraz AB . Przeciwprostokątna 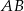AB ma długość 20 cm, a długości przyprostokątnych pozostają w stosunku 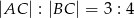|AC | : |BC | = 3 : 4 . Oblicz obwód trójkąta PBC .

PIC

Wersja PDF

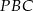Rozwiązanie

Zacznijmy od obliczenia długości przyprostokątnych trójkąta 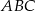ABC .

PIC

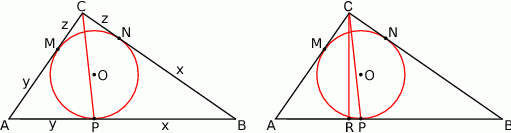
Z podanej proporcji wiemy, że 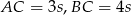AC = 3s ,BC = 4s dla pewnej liczby s . Piszemy teraz twierdzenie Pitagorasa.

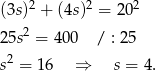
(3s)2 + (4s)2 = 20 2 2 25s = 400 / : 25 s2 = 1 6 ⇒ s = 4.

Przyprostokątne mają więc długości 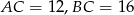AC = 12,BC = 16 .

Oznaczmy teraz 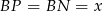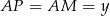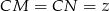BP = BN = x , AP = AM = y , CM = CN = z . Mamy więc

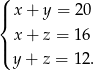
( |{ x + y = 20 x + z = 16 |( y + z = 12.

Odejmujemy od drugiego równania trzecie (żeby skrócić z ) i mamy

x − y = 4.

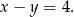
Otrzymane równanie dodajemy do pierwszego równania układu i mamy

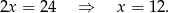
2x = 24 ⇒ x = 12.

Brakuje nam jeszcze długości odcinka 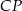CP – obliczymy ją z trójkąta prostokątnego 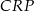CRP , gdzie 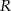R jest spodkiem wysokości opuszczonej z kąta prostego. Zanim to jednak zrobimy, obliczmy długość odcinka 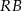RB . Z podobieństwa trójkątów 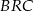BRC i BCA mamy

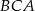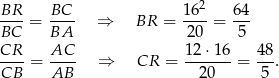
BR-- BC-- 162- 64- BC = BA ⇒ BR = 2 0 = 5 CR AC 12 ⋅16 48 ----= ---- ⇒ CR = -------= ---. CB AB 20 5

Mamy zatem

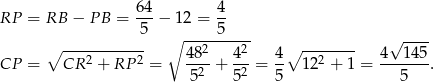
64 4 RP = RB − PB = ---− 12 = -- 5 ∘ -----5---- √ ---- ∘ ---2------2- 482- 42- 4∘ --2----- 4--1-45 CP = CR + RP = 52 + 52 = 5 12 + 1 = 5 .

Zatem obwód trójkąta 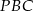PBC wynosi

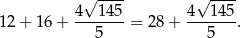
4√ 145- 4√ 14-5 1 2+ 1 6+ -------= 28 + -------. 5 5

 
Odpowiedź: 4√ 145 28 + --5-- cm

Wersja PDF