Zadanie nr 9174563
W trójkąt prostokątny 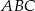 o przyprostokątnych długości
o przyprostokątnych długości 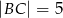 i
i 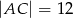 wpisano okrąg. Oblicz długość odcinka łączącego punkty wspólne okręgu wpisanego z bokami
wpisano okrąg. Oblicz długość odcinka łączącego punkty wspólne okręgu wpisanego z bokami 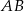 i
i 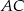 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
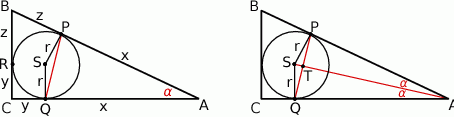
Obliczmy na początek długość przeciwprostokątnej i 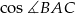 .
.
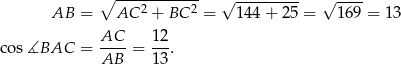
Sposób I
Długość odcinka 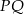 obliczymy stosując twierdzenie cosinusów w trójkącie
obliczymy stosując twierdzenie cosinusów w trójkącie 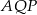 . Aby to zrobić musimy jednak najpierw obliczyć długość odcinka
. Aby to zrobić musimy jednak najpierw obliczyć długość odcinka 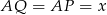 . Aby obliczyć długość tego odcinka oznaczmy przez
. Aby obliczyć długość tego odcinka oznaczmy przez 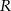 punkt styczności okręgu wpisanego z bokiem
punkt styczności okręgu wpisanego z bokiem 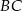 i niech
i niech 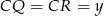 ,
, 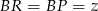 . Mamy wtedy układ równań.
. Mamy wtedy układ równań.
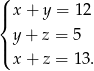
Odejmując od trzeciego równania drugie (żeby skrócić  ) mamy
) mamy
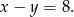
Dodajemy to do pierwszego równania (żeby skrócić 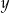 ) i mamy
) i mamy
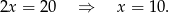
Pozostało zastosować twierdzenie cosinusów.
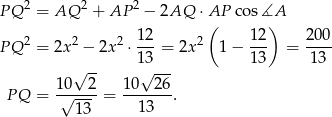
Sposób II
Tym razem dorysujmy odcinek 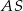 i niech
i niech 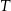 będzie punktem wspólnym odcinków
będzie punktem wspólnym odcinków 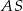 i
i 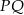 . Zauważmy, że trójkąty prostokątne
. Zauważmy, że trójkąty prostokątne 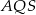 i
i 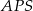 są przystające (bo odcinek
są przystające (bo odcinek 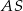 jest dwusieczną kąta
jest dwusieczną kąta 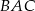 ), więc
), więc 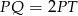 i odcinek
i odcinek 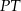 jest wysokością trójkąta
jest wysokością trójkąta 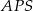 . Aby móc obliczyć długość odcinka
. Aby móc obliczyć długość odcinka 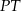 obliczymy długość promienia
obliczymy długość promienia  okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 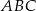 i
i 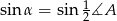 .
.
Promień okręgu wpisanego  obliczamy ze wzoru
obliczamy ze wzoru 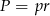 , gdzie
, gdzie 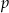 jest połową obwodu trójkąta.
jest połową obwodu trójkąta.
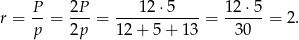
Aby obliczyć 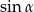 korzystamy ze wzoru
korzystamy ze wzoru
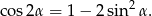
Mamy zatem
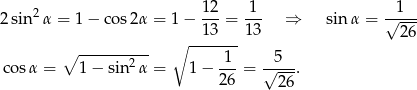
Patrzymy teraz na trójkąt prostokątny 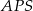 .
.
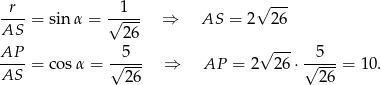
Teraz długość odcinka 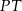 obliczamy porównując dwa wzory na pole trójkąta
obliczamy porównując dwa wzory na pole trójkąta 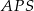 .
.
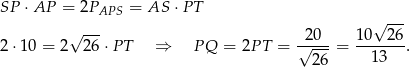
Odpowiedź: