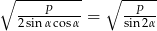Zadanie nr 9237079
W trójkącie prostokątnym dany jest kąt ostry o mierze  i pole
i pole 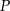 tego trójkąta. Obliczyć długość środkowej poprowadzonej z wierzchołka kąta prostego.
tego trójkąta. Obliczyć długość środkowej poprowadzonej z wierzchołka kąta prostego.
Rozwiązanie
Zauważmy, że w każdym trójkącie prostokątnym długość środkowej poprowadzonej z wierzchołka kąta prostego to dokładnie połowa przeciwprostokątnej. Aby to zobaczyć dorysujmy sobie okrąg opisany na trójkącie – jego środek to środek przeciwprostokątnej, a promień to połowa jej długości.
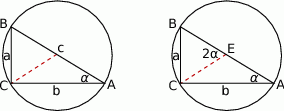
Musimy zatem policzyć długość przeciwprostokątnej.
Sposób I
Plan jest następujący – korzystając z podanego kąta wyliczymy długości przyprostokątnych  i
i 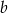 w zależności od
w zależności od  , a potem z podanego pola wyliczymy
, a potem z podanego pola wyliczymy  .
.
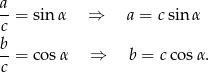
Zatem
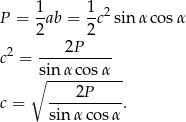
Szukana długość środkowej to połowa tej wartości.
Sposób II
Tym razem dokładniej przyjrzyjmy się trójkątowi równoramiennemu 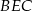 . Ma on wspólną podstawę z trójkątem
. Ma on wspólną podstawę z trójkątem 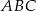 a jego wysokość opuszczona na bok
a jego wysokość opuszczona na bok 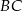 ma długość równą
ma długość równą 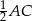 . Zatem pole trójkąta
. Zatem pole trójkąta 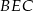 jest równe
jest równe 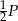 . Ponadto
. Ponadto 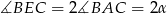 (kąty wpisany i środkowy oparte na tym samym łuku). Mamy zatem równość
(kąty wpisany i środkowy oparte na tym samym łuku). Mamy zatem równość
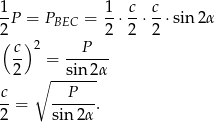
Odpowiedź: