Zadanie nr 9429829
Dany jest trójkąt prostokątny 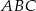 , w którym
, w którym 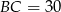 ,
, 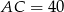 i
i 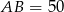 . Okrąg wpisany w trójkąt
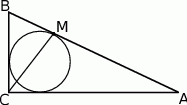
. Okrąg wpisany w trójkąt 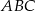 jest styczny do boku
jest styczny do boku 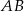 w punkcie
w punkcie 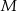 . Oblicz długość odcinka
. Oblicz długość odcinka 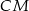 .
.
Rozwiązanie
Sposób I
Poprowadźmy wysokość 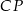 danego trójkąta.
danego trójkąta.
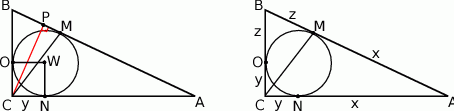
Długość odcinka 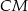 obliczymy z trójkąta prostokątnego
obliczymy z trójkąta prostokątnego 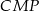 . Zanim jednak zajmiemy się tym trójkątem, popatrzmy na trójkąt prostokątny
. Zanim jednak zajmiemy się tym trójkątem, popatrzmy na trójkąt prostokątny 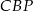 . Ponieważ jest on podobny do wyjściowego trójkąta (bo oba są prostokątne i mają wspólny kąt
. Ponieważ jest on podobny do wyjściowego trójkąta (bo oba są prostokątne i mają wspólny kąt 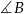 ), łatwo można wyliczyć długości jego boków.
), łatwo można wyliczyć długości jego boków.
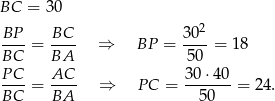
Skoro znamy długość 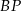 , to długość odcinka
, to długość odcinka 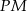 możemy obliczyć jako różnicę długości
możemy obliczyć jako różnicę długości 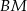 i
i 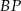 . Do tego jednak musimy znać długość
. Do tego jednak musimy znać długość 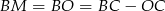 . Długość
. Długość 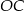 to po prostu długość
to po prostu długość  promienia okręgu wpisanego w trójkąt
promienia okręgu wpisanego w trójkąt 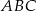 , którą możemy obliczyć ze wzoru na pole:
, którą możemy obliczyć ze wzoru na pole: 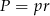 , gdzie
, gdzie 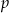 jest połową obwodu trójkąta.
jest połową obwodu trójkąta.
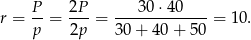
Mamy więc
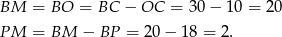
Pozostało zastosować twierdzenie Pitagorasa w trójkącie 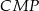 .
.
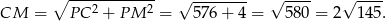
Sposób II
Długość odcinka 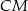 możemy obliczyć z twierdzenia cosinusów w trójkącie
możemy obliczyć z twierdzenia cosinusów w trójkącie 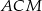 . Zanim to jednak zrobimy, musimy wyliczyć
. Zanim to jednak zrobimy, musimy wyliczyć 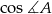 i
i 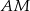 .
.
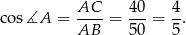
Aby obliczyć długość odcinka 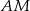 , zaznaczmy pozostałe punkty styczności okręgu wpisanego z bokami trójkąta i oznaczmy
, zaznaczmy pozostałe punkty styczności okręgu wpisanego z bokami trójkąta i oznaczmy 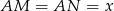 ,
, 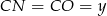 i
i 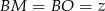 . Mamy wtedy układ równań.
. Mamy wtedy układ równań.

Odejmując od drugiego równania trzecie (żeby skrócić  ) mamy
) mamy
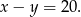
Dodajemy to do pierwszego równania (żeby skrócić 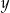 ) mamy
) mamy
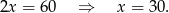
Pozostało zastosować twierdzenie cosinusów.
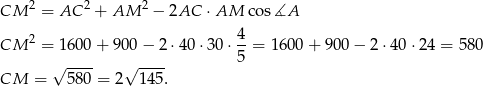
Odpowiedź: