Definicje Ustalmy dwa zbiory: 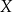 i
i 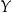 .
.
Funkcją określoną na zbiorze 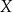 i o wartościach w zbiorze
i o wartościach w zbiorze 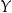 nazywamy dowolne przyporządkowanie, które każdemu elementowi zbioru
nazywamy dowolne przyporządkowanie, które każdemu elementowi zbioru 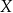 przyporządkowuje pewien element zbioru
przyporządkowuje pewien element zbioru 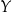 .
.
Jeżeli 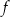 jest funkcją spełniającą powyższą definicję to zbiór
jest funkcją spełniającą powyższą definicję to zbiór 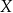 nazywamy dziedziną funkcji
nazywamy dziedziną funkcji 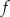 , a zbiór
, a zbiór 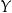 jej przeciwdziedziną.
jej przeciwdziedziną.
Jeżeli chcemy wyraźnie zaznaczyć jaka jest dziedzina lub przeciwdziedzina funkcji to używamy zapisu
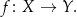
Podkreślmy, że funkcja 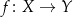 musi każdemu elementowi zbioru
musi każdemu elementowi zbioru 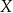 przyporządkować dokładnie jeden element zbioru
przyporządkować dokładnie jeden element zbioru 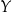 . Z drugiej strony, nie wszystkie elementy zbioru
. Z drugiej strony, nie wszystkie elementy zbioru 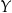 muszą być przyporządkowane pewnym elementom zbioru
muszą być przyporządkowane pewnym elementom zbioru 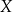 .
.
Przyporządkowanie każdej osobie jej wieku jest funkcją określoną na zbiorze wszystkich ludzi.
Przyporządkowanie każdej osobie imienia jednego z jej braci nie jest funkcją, bo są osoby, które nie mają braci.
Wystarczy jednak, że ograniczymy to przyporządkowanie do osób, które mają braci (czyli zmienimy zbiór 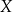 ) i już dostaniemy funkcję.
) i już dostaniemy funkcję.
Jeżeli funkcja 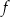 przyporządkowuje elementowi
przyporządkowuje elementowi 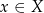 element
element 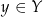 to piszemy
to piszemy 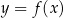 i mówimy, że
i mówimy, że 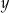 jest wartością funkcji
jest wartością funkcji 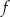 dla argumentu
dla argumentu  . Zbiór wszystkich wartości funkcji
. Zbiór wszystkich wartości funkcji 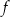 nazywamy jej zbiorem wartości i oznaczamy symbolem
nazywamy jej zbiorem wartości i oznaczamy symbolem 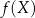 – jest to zawsze podzbiór przeciwdziedziny
– jest to zawsze podzbiór przeciwdziedziny 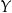 . Różne sposoby określenia funkcji 1. Opis słowny. Tego typu definicje funkcji stosujemy co rusz w naszym codziennym życiu, często nie zdając sobie nawet z tego sprawy.
. Różne sposoby określenia funkcji 1. Opis słowny. Tego typu definicje funkcji stosujemy co rusz w naszym codziennym życiu, często nie zdając sobie nawet z tego sprawy.
Aktualna wartość indeksu giełdowego WIG20 w kolejnych dniach – za dziedzinę tej funkcji możemy przyjąć kartki kalendarza:)
Wzrost – funkcja określona na zbiorze wszystkich ludzi.
2. Graf. Tego typu definicje trudno znaleźć poza kartami podręczników do matematyki, ale mają one duży walor dydaktyczny, bo pozwalają łatwo obrazować różne własności funkcji.
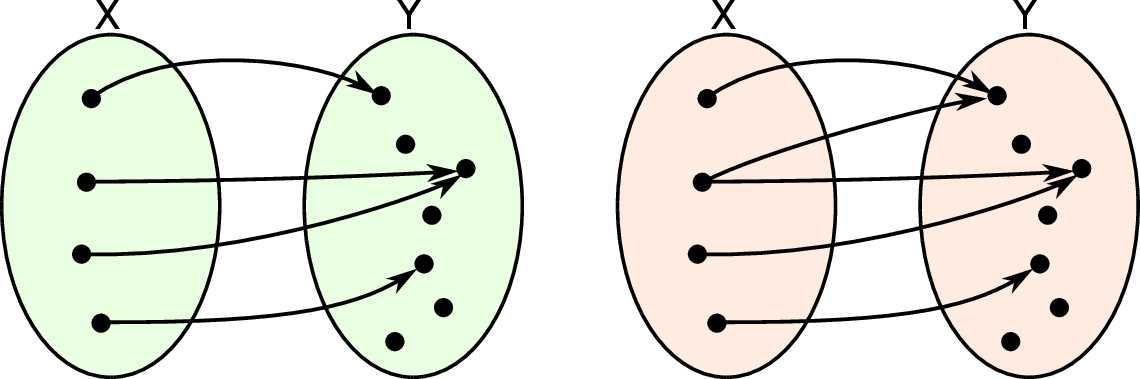
Na pierwszym z poniższych diagramów mamy zaznaczone przyporządkowanie elementom zbioru 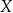 elementy zbioru
elementy zbioru 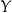 , które jest funkcją. Przyporządkowanie z drugiego diagramu nie jest funkcją, bo jednemu z elementów zbioru
, które jest funkcją. Przyporządkowanie z drugiego diagramu nie jest funkcją, bo jednemu z elementów zbioru  przyporządkowano dwa elementy zbioru
przyporządkowano dwa elementy zbioru  .
.
3. Tabelka. Jeżeli zbiór  zawiera tylko skończenie wiele elementów, to całą funkcję możemy zapisać w tabelce. Tego typu sytuacja występuje dość często w przypadku wyników pomiarów.
zawiera tylko skończenie wiele elementów, to całą funkcję możemy zapisać w tabelce. Tego typu sytuacja występuje dość często w przypadku wyników pomiarów.
Powiedzmy, że chcemy ustalić jak zmienia się ciśnienie atmosferyczne na kolejnych piętrach 10 piętrowego budynku. Wyniki takiego doświadczenia najwygodniej zanotować w tabeli.
| piętro | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| ciśnienie |
4. Wzór. Typowa sytuacja w przypadku funkcji liczbowych. Mając wzór funkcji 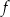 , czyli przepis na obliczanie jej wartości, możemy stosować różne matematyczne metody badania funkcji. Dział matematyki poświęcony temu zagadnieniu nazywa się analizą matematyczną.
, czyli przepis na obliczanie jej wartości, możemy stosować różne matematyczne metody badania funkcji. Dział matematyki poświęcony temu zagadnieniu nazywa się analizą matematyczną.
Wzór 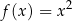 możemy przeczytać: funkcja
możemy przeczytać: funkcja 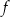 zamienia liczbę na jej kwadrat.
zamienia liczbę na jej kwadrat.
W przypadku funkcji określonych wzorem, zazwyczaj nie podaje się wyraźnie dziedziny funkcji. W takiej sytuacji domyślnie rozumiemy, że dziedzina jest największa możliwa, czyli jest to zbiór wszystkich liczb, dla których dany wzór ma sens.
Wzór 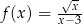 nie ma sensu dla
nie ma sensu dla 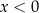 oraz dla
oraz dla 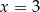 , zatem za dziedzinę przyjmujemy
, zatem za dziedzinę przyjmujemy 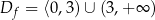 .
.
5. Wykres. Dość popularny motyw zadań szkolnych to odczytywanie własności funkcji z danego wykresu. Więcej na ten temat znajdziecie w poradniku dotyczącym wykresów funkcji.
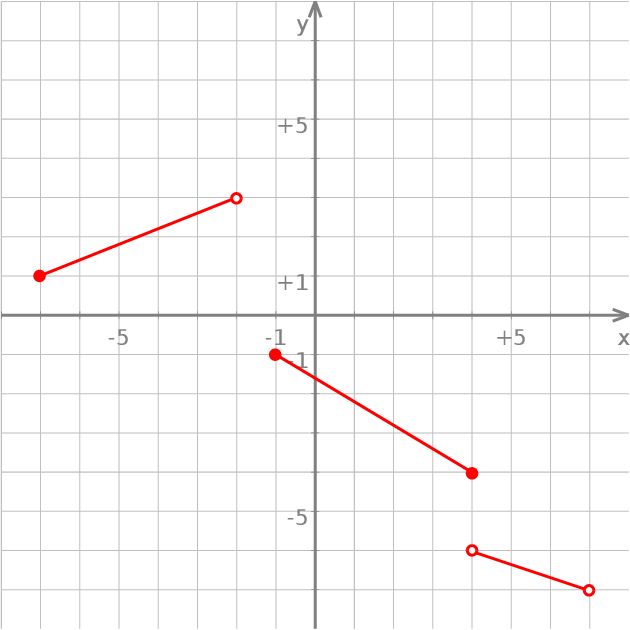
Z poniższego wykresu funkcji 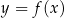 odczytujemy jej dziedzinę:
odczytujemy jej dziedzinę: 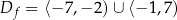 oraz zbiór wartości:
oraz zbiór wartości: 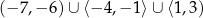 .
.
Monotoniczność Niech  będzie funkcją liczbową, a
będzie funkcją liczbową, a 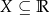 pewnym przedziałem zawartym w dziedzinie
pewnym przedziałem zawartym w dziedzinie 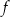 .
.
Mówimy, że funkcja 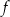 jest rosnąca na przedziale
jest rosnąca na przedziale 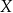 , jeżeli dla dowolnych
, jeżeli dla dowolnych 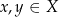 spełniona jest implikacja
spełniona jest implikacja
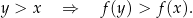
Powyższy warunek należy zapamiętać w formie: dla większych argumentów funkcja przyjmuje większe wartości.
Uzasadnijmy, że funkcja dana wzorem 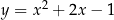 jest rosnąca na przedziale
jest rosnąca na przedziale 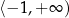 .
.
Jeżeli założymy, że 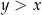 to
to
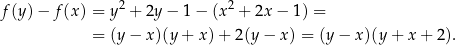
Z założenia 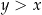 wynika, że pierwszy nawias jest dodatni. Dodatniość drugiego nawiasu wynika z warunku
wynika, że pierwszy nawias jest dodatni. Dodatniość drugiego nawiasu wynika z warunku 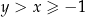 . W takim razie liczba z prawej strony nierówności jest dodatnia, co oznacza, że
. W takim razie liczba z prawej strony nierówności jest dodatnia, co oznacza, że 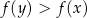 .
.
Mówimy, że funkcja 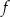 jest malejąca na przedziale
jest malejąca na przedziale 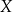 , jeżeli dla dowolnych
, jeżeli dla dowolnych 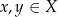 spełniona jest implikacja
spełniona jest implikacja
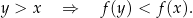
Powyższy warunek należy zapamiętać w formie: dla większych argumentów funkcja przyjmuje mniejsze wartości.
Uzasadnijmy, że funkcja 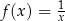 jest malejąca na przedziale
jest malejąca na przedziale 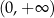 .
.
Jeżeli założymy, że 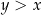 to
to
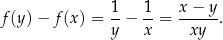
Na mocy założenia: 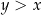 i
i 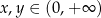 , więc licznik jest ujemny, a mianownik dodatni. Zatem
, więc licznik jest ujemny, a mianownik dodatni. Zatem 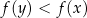 .
.
Mówimy, że funkcja 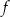 jest monotoniczna na przedziale
jest monotoniczna na przedziale 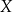 jeżeli jest na tym przedziale rosnąca lub malejąca.
jeżeli jest na tym przedziale rosnąca lub malejąca.
Uzasadnijmy, że funkcja 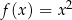 nie jest monotoniczna na zbiorze
nie jest monotoniczna na zbiorze 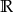 .
.
Aby wykazać, że funkcja nie jest rosnąca wystarczy pokazać przykład dwóch liczb 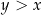 , dla których
, dla których 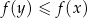 . Łatwo to zrobić:
. Łatwo to zrobić: 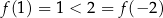 , pomimo, że
, pomimo, że 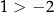 .
.
Podobnie pokazujemy, że funkcja nie jest malejąca: wystarczy pokazać dwie liczby 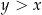 , dla których
, dla których 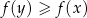 . Na przykład
. Na przykład 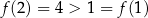 oraz
oraz 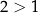 .
.
Parzystość Niech 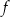 będzie funkcją zdefiniowaną na zbiorze
będzie funkcją zdefiniowaną na zbiorze 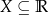 oraz załóżmy, że zbiór
oraz załóżmy, że zbiór 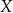 ma następującą własność: jeżeli
ma następującą własność: jeżeli 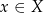 to
to 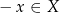 . Geometrycznie to dodatkowe założenie oznacza, że zbiór
. Geometrycznie to dodatkowe założenie oznacza, że zbiór 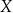 (jako podzbiór osi
(jako podzbiór osi 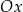 ) jest symetryczny względem punktu
) jest symetryczny względem punktu 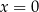 .
.
Funkcja 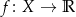 jest funkcją parzystą jeżeli dla dowolnego
jest funkcją parzystą jeżeli dla dowolnego 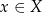
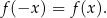
Innymi słowy, wartość funkcji w 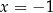 jest taka sama jak wartość w
jest taka sama jak wartość w 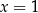 , wartość w
, wartość w 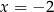 jest taka sama jak wartość w
jest taka sama jak wartość w 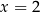 itd.
itd.
Uzasadnijmy, że funkcja dana wzorem 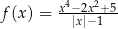 jest parzysta.
jest parzysta.
Łatwo sprawdzić, że dziedziną funkcji jest zbiór 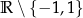 , który jest symetryczny względem
, który jest symetryczny względem 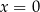 . Pozostało sprawdzić, że
. Pozostało sprawdzić, że 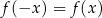 . Liczymy
. Liczymy
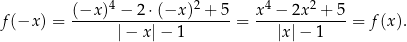
Funkcja 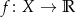 jest funkcją nieparzystą jeżeli dla dowolnego
jest funkcją nieparzystą jeżeli dla dowolnego 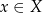
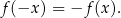
Sprawdźmy, że funkcja dana wzorem 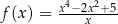 jest nieparzysta.
jest nieparzysta.
Dziedziną jest zbiór 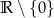 , który jest symetryczny względem
, który jest symetryczny względem 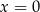 . Pozostało sprawdzić, że
. Pozostało sprawdzić, że 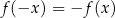 . Liczymy
. Liczymy
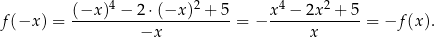
Funkcje 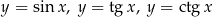 są nieparzyste, a funkcja
są nieparzyste, a funkcja 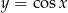 jest parzysta.
jest parzysta.
Funkcja 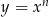 , gdzie
, gdzie 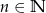 jest parzysta wtedy i tylko wtedy, gdy
jest parzysta wtedy i tylko wtedy, gdy  jest liczbą parzystą. Funkcja ta jest nieparzysta wtedy i tylko wtedy, gdy
jest liczbą parzystą. Funkcja ta jest nieparzysta wtedy i tylko wtedy, gdy  jest liczbą nieparzystą.
jest liczbą nieparzystą.
Aby wykazać, że funkcja 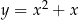 nie jest parzysta, wystarczy podać przykład wartości
nie jest parzysta, wystarczy podać przykład wartości  , dla której
, dla której 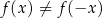 . Żaden problem:
. Żaden problem:
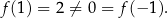
Zauważmy, że ten sam przykład pokazuje, że funkcja 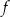 nie jest nieparzysta.
nie jest nieparzysta.
Okresowość Niech 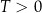 .
.
Funkcja 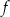 jest funkcją okresową o okresie
jest funkcją okresową o okresie 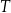 jeżeli dla dowolnego
jeżeli dla dowolnego 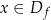
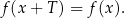
Powyższy warunek zwykle pamięta się w formie: wartości funkcji powtarzają się co 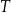 . Jeżeli istnieje najmniejsza liczba
. Jeżeli istnieje najmniejsza liczba 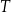 o powyższej własności, to liczbę tę nazywamy okresem podstawowym funkcji
o powyższej własności, to liczbę tę nazywamy okresem podstawowym funkcji 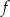 .
.
Funkcja 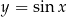 jest okresowa i jej okres podstawowy jest równy
jest okresowa i jej okres podstawowy jest równy 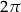 .
.
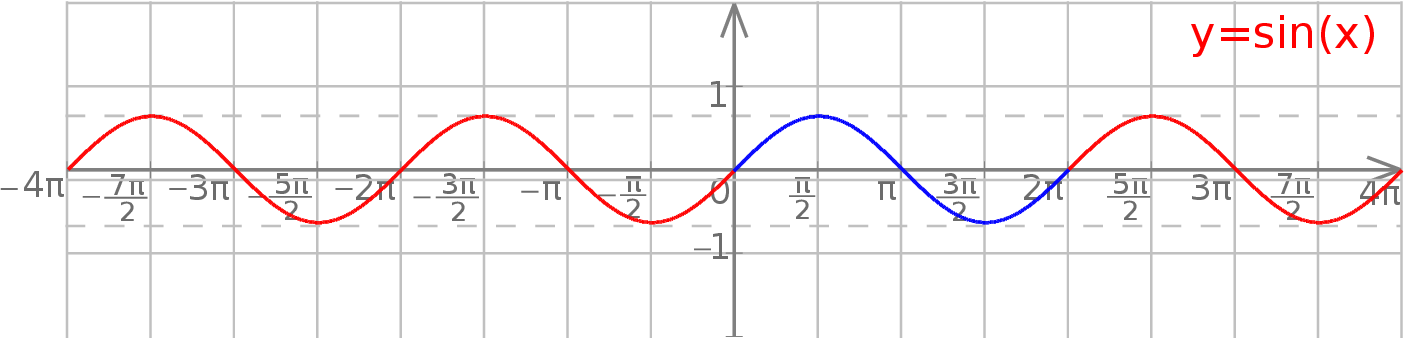
Okresowość widać wyraźnie na wykresie: znając tylko kawałek wykresu położony nad przedziałem 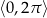 jesteśmy w stanie odtworzyć cały wykres – wystarczy przesuwać ten kawałek o wielokrotności
jesteśmy w stanie odtworzyć cały wykres – wystarczy przesuwać ten kawałek o wielokrotności 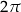 .
.
Zauważmy jeszcze, że każda dodatnia wielokrotność liczby 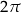 też jest okresem funkcji
też jest okresem funkcji 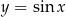 . Jednak tylko
. Jednak tylko 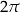 jest okresem podstawowym (bo jest to najmniejszy możliwy okres).
jest okresem podstawowym (bo jest to najmniejszy możliwy okres).
Wyznaczmy okres podstawowy funkcji 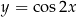 .
.
Szukamy najmniejszej liczby 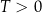 , dla której
, dla której
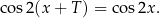
Korzystając ze wzoru na różnicę cosinusów mamy
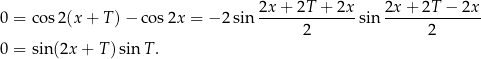
Powyższa równość ma być spełniona dla dowolnej wartości  , czyli zerowy musi być drugi składnik (bo są wartości
, czyli zerowy musi być drugi składnik (bo są wartości  , dla których pierwszy składnik jest niezerowy). Zatem
, dla których pierwszy składnik jest niezerowy). Zatem 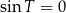 . Najmniejszą liczbą dodatnią spełniającą ten warunek jest
. Najmniejszą liczbą dodatnią spełniającą ten warunek jest 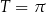 .
.
Różnowartościowość Funkcja jest różnowartościowa jeżeli dla różnych argumentów przyjmuje różne wartości. Formalnie zapisujemy to następująco
Funkcja 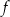 jest różnowartościowa jeżeli dla dowolnych
jest różnowartościowa jeżeli dla dowolnych 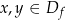
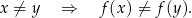
W języku grafów, funkcja jest różnowartościowa, jeżeli żadne dwie strzałki nie prowadzą do tego samego punktu.
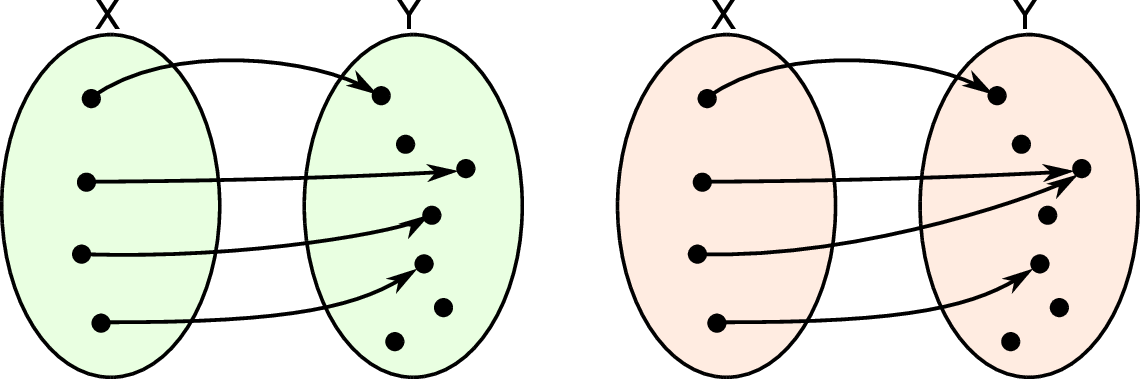
Na przykład funkcja przedstawiona na lewym obrazku jest różnowartościowa, a funkcja z prawego obrazka nie jest.
Funkcja 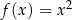 nie jest różnowartościowa, bo na przykład
nie jest różnowartościowa, bo na przykład
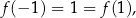
pomimo, że 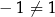 .
.
Warto zapamiętać, że funkcje monotoniczne są różnowartościowe.
Jeżeli funkcja 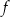 jest monotoniczna na zbiorze
jest monotoniczna na zbiorze 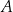 , to jest ona na tym zbiorze różnowartościowa.
, to jest ona na tym zbiorze różnowartościowa.
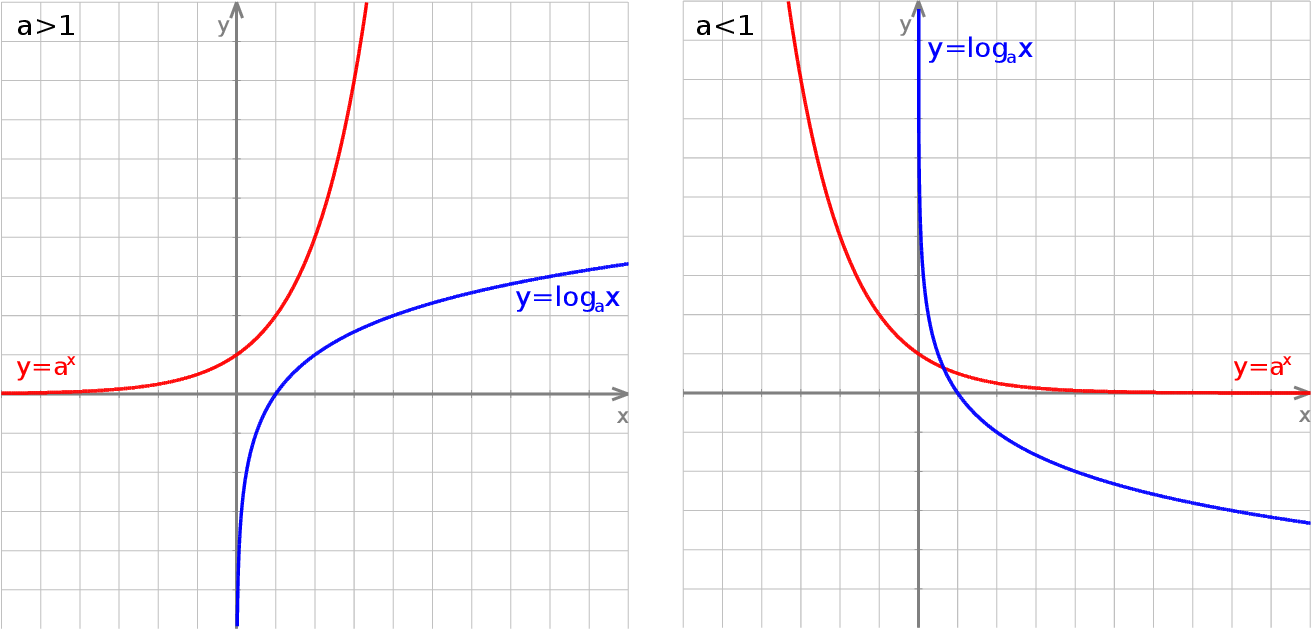
Można udowodnić, że funkcje wykładnicze 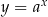 i logarytmiczne
i logarytmiczne 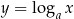 są monotoniczne (rosnące dla
są monotoniczne (rosnące dla  i malejące dla
i malejące dla  ), są więc różnowartościowe.
), są więc różnowartościowe.
Bycie „na” Własność, o której chcemy mówić w tym rozdziale jest odrobinę bardziej egzotyczna od poprzednich, bo w zasadzie jest to bardziej własność zapisu 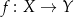 , niż własność samego przyporządkowania. Dokładniej,
, niż własność samego przyporządkowania. Dokładniej,
mówimy, że funkcja 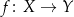 jest „na” zbiór
jest „na” zbiór 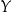 jeżeli
jeżeli 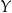 jest zbiorem wartości
jest zbiorem wartości 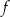 .
.
Innymi słowy, funkcja jest „na” 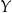 , jeżeli każdy element
, jeżeli każdy element 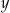 zbioru
zbioru 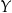 jest postaci
jest postaci 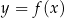 dla pewnego
dla pewnego 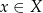 .
.
Funkcja 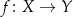 przedstawiona na lewym diagramie jest „na” zbiór
przedstawiona na lewym diagramie jest „na” zbiór 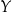 .
.
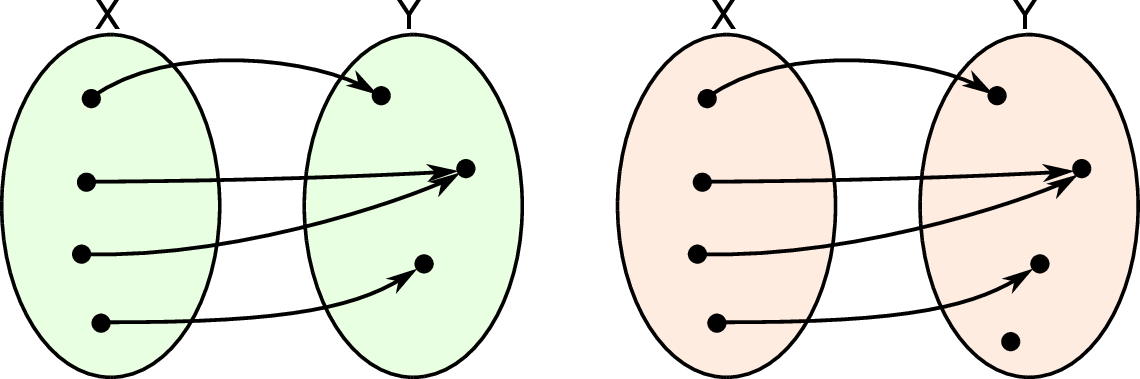
Natomiast funkcja z prawego diagramu nie jest „na”, bo jest  -ek, który nie jest wartością funkcji.
-ek, który nie jest wartością funkcji.
Funkcja 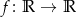 dana wzorem
dana wzorem 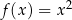 nie jest „na”, bo np.
nie jest „na”, bo np. 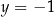 nie jest wartością funkcji
nie jest wartością funkcji 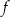 .
.
Jeżeli jednak tę samą funkcję zapiszemy w postaci 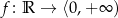 to jest to już funkcja „na”.
to jest to już funkcja „na”.
Każda funkcja jest „na” swój zbiór wartości.
Funkcję 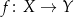 , która jest jednocześnie różnowartościowa i „na” nazywamy funkcją wzajemnie jednoznaczną.
, która jest jednocześnie różnowartościowa i „na” nazywamy funkcją wzajemnie jednoznaczną.

