Zadanie nr 3303166
Dwa wierzchołki prostokąta leżą na osi  , a pozostałe dwa należą do paraboli o równaniu
, a pozostałe dwa należą do paraboli o równaniu 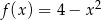 i znajdują się powyżej osi
i znajdują się powyżej osi  .
.
- Podaj wzór funkcji opisującej pole tego prostokąta w zależności od jego podstawy.
- Dla jakiej długości podstawy pole tego prostokąta jest równe 6.
- Dla jakiej długości podstawy pole tego prostokąta jest największe?
Rozwiązanie
Zacznijmy od rysunku.
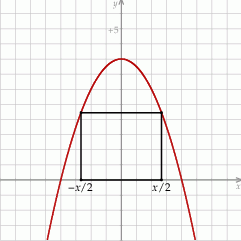
- Jeżeli przez
 oznaczymy długość podstawy, to wierzchołki na osi
oznaczymy długość podstawy, to wierzchołki na osi  mają współrzędne
mają współrzędne 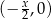 i
i 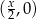 , gdzie
, gdzie 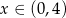 . Stąd wyliczamy współrzędne wierzchołków na paraboli (tak naprawdę potrzebny nam jest tylko jeden z nich):
. Stąd wyliczamy współrzędne wierzchołków na paraboli (tak naprawdę potrzebny nam jest tylko jeden z nich): 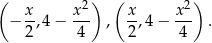
Liczymy pole
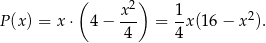
Odpowiedź: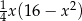
- Rozwiązujemy równanie
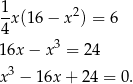
Szukamy pierwiastków całkowitych tego równania wśród dzielników wyrazu wolnego. Sprawdzając znajdujemy pierwiastek
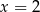 . Dzielimy teraz ten wielomian przez
. Dzielimy teraz ten wielomian przez 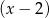 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy. 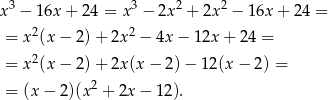
Rozwiązujemy równanie kwadratowe
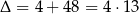 . Stąd dodatni pierwiastek to
. Stąd dodatni pierwiastek to 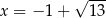 .
. Zauważmy, że oba znalezione pierwiastki spełniają nierówność
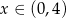 .
.
Odpowiedź: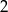 lub
lub 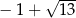
- Szukamy punktu, w którym funkcja
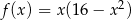 przyjmuje wartość największą w przedziale
przyjmuje wartość największą w przedziale 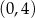 . Liczymy pochodną funkcji
. Liczymy pochodną funkcji 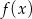 .
. 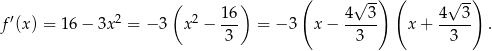
Wykresem tej funkcji jest parabola o ramionach skierowanych w dół. Widzimy zatem, że pochodna jest dodatnia na przedziale
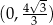 (czyli funkcja
(czyli funkcja 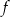 rośnie) i ujemna na przedziale
rośnie) i ujemna na przedziale 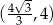 (czyli funkcja
(czyli funkcja 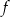 maleje). Wartość największa jest zatem osiągana dla
maleje). Wartość największa jest zatem osiągana dla 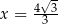 .
.
Odpowiedź: