Zadanie nr 7945833
Rozpatrujemy wszystkie prostokąty 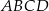 , których dwa wierzchołki
, których dwa wierzchołki 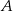 i
i 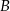 leżą na odcinku o końcach
leżą na odcinku o końcach 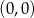 i
i 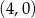 , a dwa pozostałe wierzchołki
, a dwa pozostałe wierzchołki 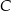 i
i 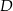 leżą na paraboli o równaniu
leżą na paraboli o równaniu 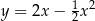 (zobacz rysunek).
(zobacz rysunek).
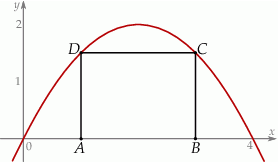
Oblicz obwód tego z rozpatrywanych prostokątów, którego pole jest największe.
Rozwiązanie
Jeżeli oznaczymy 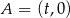 to
to 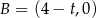 ,
, 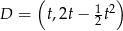 . Stąd
. Stąd
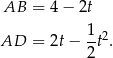
Pole prostokąta jest więc równe
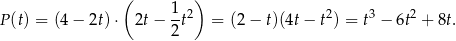
Dziedziną tej funkcji jest przedział 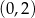 . Liczymy jej pochodną.
. Liczymy jej pochodną.
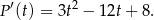
Rozkładamy otrzymany trójmian.
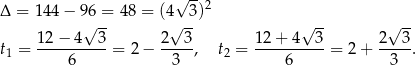
To oznacza, że na przedziale 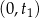 pochodna jest dodatnia, a na przedziale
pochodna jest dodatnia, a na przedziale 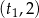 pochodna jest ujemna. To z kolei oznacza, że funkcja
pochodna jest ujemna. To z kolei oznacza, że funkcja 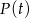 rośnie na przedziale
rośnie na przedziale 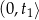 i maleje na przedziale
i maleje na przedziale 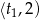 . Największe pole otrzymamy więc dla
. Największe pole otrzymamy więc dla 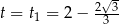 . Mamy wtedy
. Mamy wtedy
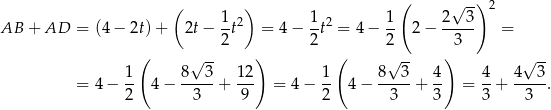
Obwód prostokąta jest dwa razy większy
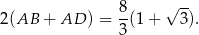
Odpowiedź: