Zadanie nr 8983865
Parabola o równaniu 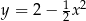 przecina oś
przecina oś 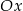 układu współrzędnych w punktach
układu współrzędnych w punktach 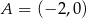 i
i 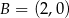 . Rozpatrujemy wszystkie trapezy równoramienne
. Rozpatrujemy wszystkie trapezy równoramienne 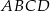 , których dłuższą podstawą jest odcinek
, których dłuższą podstawą jest odcinek 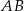 , a końce
, a końce 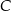 i
i  krótszej podstawy leżą na paraboli (zobacz rysunek).
krótszej podstawy leżą na paraboli (zobacz rysunek).
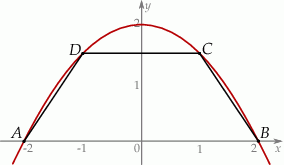
Wyznacz pole trapezu 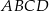 w zależności od pierwszej współrzędnej wierzchołka
w zależności od pierwszej współrzędnej wierzchołka 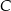 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 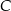 tego z rozpatrywanych trapezów, którego pole jest największe.
tego z rozpatrywanych trapezów, którego pole jest największe.
Rozwiązanie
Jeżeli oznaczymy 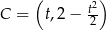 , to
, to 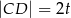 ,
, 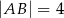 i wysokość trapezu jest równa
i wysokość trapezu jest równa
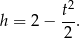
Pole trapezu jest więc równe
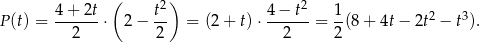
Dziedziną tej funkcji jest przedział 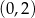 . Liczymy jej pochodną.
. Liczymy jej pochodną.
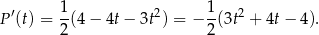
Rozkładamy trójmian w nawiasie.
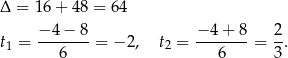
Zatem
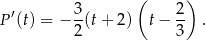
To oznacza, że na przedziale 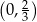 pochodna jest dodatnia, a na przedziale
pochodna jest dodatnia, a na przedziale 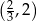 pochodna jest ujemna. To oznacza, że funkcja
pochodna jest ujemna. To oznacza, że funkcja 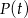 rośnie na przedziale
rośnie na przedziale 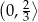 i maleje na przedziale
i maleje na przedziale 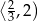 . Największe pole otrzymamy więc dla
. Największe pole otrzymamy więc dla 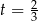 . Wierzchołek
. Wierzchołek 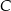 ma wtedy współrzędne
ma wtedy współrzędne
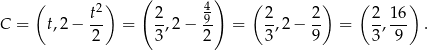
Odpowiedź: