Zadanie nr 2951398
Rozpatrujemy wszystkie trapezy 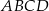 , których wierzchołki
, których wierzchołki 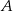 i
i 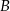 leżą na wykresie funkcji
leżą na wykresie funkcji 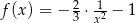 określonej dla
określonej dla 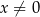 . Punkt
. Punkt 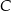 ma współrzędne
ma współrzędne 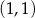 , a oś
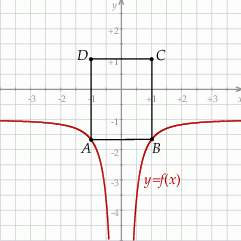
, a oś 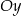 jest osią symetrii tego trapezu (zobacz rysunek).
jest osią symetrii tego trapezu (zobacz rysunek).
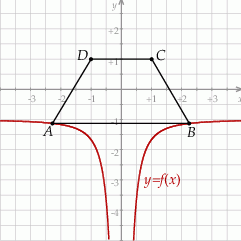
Oblicz obwód tego trapezu 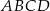 , którego pole jest najmniejsze możliwe.
, którego pole jest najmniejsze możliwe.
Rozwiązanie
Jeżeli oznaczymy 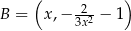 dla
dla 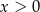 , to
, to 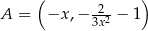 i
i 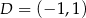 . Pole trapezu
. Pole trapezu 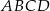 jest więc równe
jest więc równe
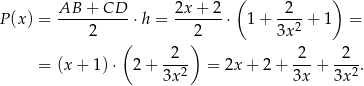
Liczymy pochodną tej funkcji
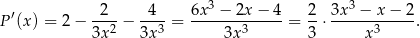
Widać teraz, że jednym z pierwiastków licznika jest 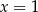 . Dzielimy więc wielomian w liczniku przez
. Dzielimy więc wielomian w liczniku przez 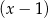 . My zrobimy to grupując wyrazy
. My zrobimy to grupując wyrazy
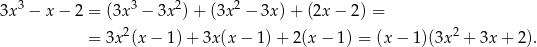
Łatwo sprawdzić, że wyrażenie w drugim nawiasie jest zawsze dodatnie (bo 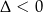 ), więc pochodna
), więc pochodna 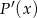 jest ujemna w przedziale
jest ujemna w przedziale 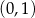 i dodatnia w przedziale
i dodatnia w przedziale 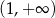 . W takim razie funkcja
. W takim razie funkcja 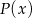 maleje w przedziale
maleje w przedziale 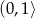 i rośnie w przedziale
i rośnie w przedziale 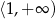 . Najmniejsze pole trapezu otrzymamy więc dla
. Najmniejsze pole trapezu otrzymamy więc dla 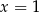 . Mamy wtedy
. Mamy wtedy
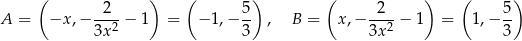
i czworokąt 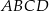 jest prostokątem o bokach długości
jest prostokątem o bokach długości 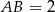 ,
, 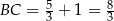 .
.
Obwód tego prostokąta jest równy
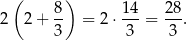
Odpowiedź: