Zadanie nr 8789998
Na krzywej 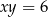 obrano punkty
obrano punkty 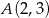 i
i 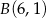 . Znajdź na tej krzywej taki punkt
. Znajdź na tej krzywej taki punkt 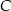 o ujemnej odciętej, aby pole trójkąta
o ujemnej odciętej, aby pole trójkąta 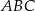 było najmniejsze.
było najmniejsze.
Rozwiązanie
Szkicujemy hiperbolę 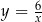 i zaznaczamy na niej podane punkty
i zaznaczamy na niej podane punkty 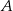 i
i  .
.
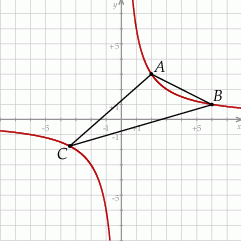
Niech 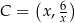 będzie dowolnym punktem lewej gałęzi tej hiperboli. Pole trójkąta
będzie dowolnym punktem lewej gałęzi tej hiperboli. Pole trójkąta 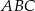 najprościej jest obliczyć korzystając ze wzoru na odległość punktu od prostej, ale zanim to zrobimy obliczamy
najprościej jest obliczyć korzystając ze wzoru na odległość punktu od prostej, ale zanim to zrobimy obliczamy
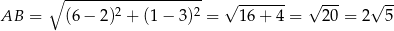
oraz wyznaczamy równanie prostej 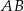 . Szukamy prostej w postaci
. Szukamy prostej w postaci 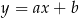 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 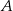 i
i 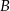 .
.
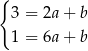
Odejmujemy od drugiego równania pierwsze i mamy
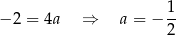
Stąd 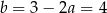 i prosta
i prosta 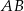 ma równanie
ma równanie
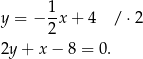
Obliczamy teraz odległość punktu 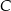 od prostej
od prostej 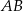 (czyli wysokość trójkąta
(czyli wysokość trójkąta 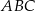 opuszczoną na bok
opuszczoną na bok 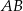 ).
).
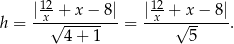
Zauważmy jeszcze, że łatwo możemy opuścić wartość bezwzględną. Możemy to zrobić geometrycznie, korzystając z tego, że punkt 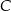 leży zawsze poniżej prostej
leży zawsze poniżej prostej 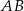 , albo algebraicznie, korzystając z tego, że
, albo algebraicznie, korzystając z tego, że 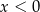 :
:
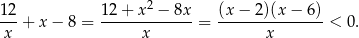
Mamy zatem
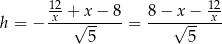
i pole trójkąta 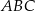 jest więc równe
jest więc równe
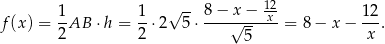
Pozostało wyznaczyć najmniejszą możliwą wartość tej funkcji określonej dla 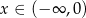 . Liczymy pochodną
. Liczymy pochodną
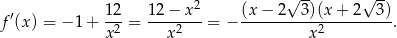
Widać teraz, że pochodna jest ujemna dla 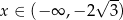 i dodatnia dla
i dodatnia dla 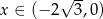 . To oznacza, że funkcja
. To oznacza, że funkcja 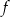 maleje na przedziale
maleje na przedziale 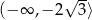 i rośnie na przedziale
i rośnie na przedziale 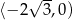 . W takim razie najmniejszą możliwą wartość funkcji
. W takim razie najmniejszą możliwą wartość funkcji 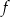 otrzymamy dla
otrzymamy dla 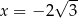 . Mamy wtedy
. Mamy wtedy
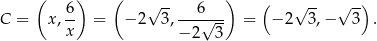
Odpowiedź: