/Szkoła średnia/Geometria/Geometria analityczna/Zadania na ekstremum/Najmniejsza długość

Zadanie nr 1988192

Na paraboli o równaniu 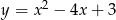2 y = x − 4x + 3 wyznacz punkt, którego odległość od prostej 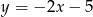y = − 2x − 5 jest najmniejsza.

Wersja PDF

Rozwiązanie

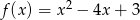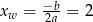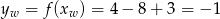Zacznijmy od szkicowego rysunku. Parabola 2 f (x) = x − 4x + 3 ma wierzchołek w punkcie o pierwszej współrzędnej równej xw = −2ba-= 2 i drugiej współrzędnej yw = f(xw ) = 4 − 8 + 3 = − 1 .

PIC

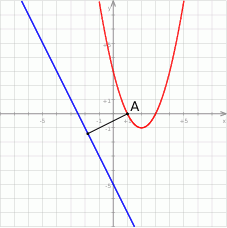
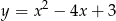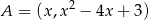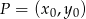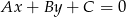Punkty paraboli y = x2 − 4x + 3 mają postać A = (x,x2 − 4x + 3) . Korzystając ze wzoru na odległość punktu P = (x0,y0) od prostej Ax + By + C = 0 :

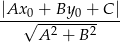
|Ax-0 +-By-0 +-C| √ --2----2- A + B

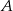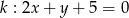liczymy odległość punktu A od danej prostej k : 2x + y + 5 = 0 .

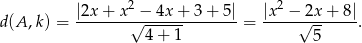
|2x + x2 − 4x+ 3+ 5| |x2 − 2x + 8| d(A ,k) = -------√--------------= -----√-------. 4 + 1 5

Zauważmy, że trójmian pod wartością bezwzględną jest zawsze dodatni (bo 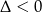Δ < 0 ), więc możemy opuścić wartość bezwzględną bez zmiany znaku.

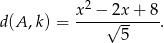
x2-−-2x-+-8- d(A ,k) = √ -- . 5

Wyrażenie to przyjmuje najmniejszą wartość w wierzchołku paraboli, która jest w liczniku, czyli dla

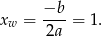
−b xw = ----= 1. 2a

Wtedy 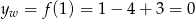yw = f(1) = 1− 4 + 3 = 0 . Szukanym punktem jest więc punkt o współrzędnych (1 ,0 ) .  
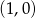Odpowiedź: (1,0)

Wersja PDF