/Szkoła średnia/Geometria/Geometria analityczna/Zadania na ekstremum/Najmniejsza długość

Zadanie nr 2064172

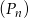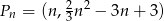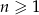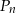Dany jest ciąg punktów (Pn) na płaszczyźnie, których współrzędne dane są wzorem Pn = (n, 23n 2 − 3n + 3) , gdzie n ≥ 1 . Wyznacz tę wartość n , dla której odległość punktu Pn od prostej 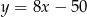y = 8x − 50 jest najmniejsza z możliwych.

Wersja PDF

Rozwiązanie

Możemy zacząć od szkicowego rysunku, ale ze względu na duże współczynniki nie jest łatwo go zrobić.

PIC

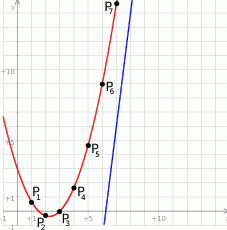
Kolejne punkty 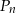Pn leżą na paraboli 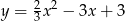y = 23x 2 − 3x + 3 , która ma wierzchołek w punkcie

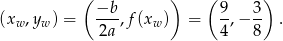
( ) ( ) (x ,y ) = −b-,f(x ) = 9,− 3- . w w 2a w 4 8

No dobrze, policzmy odległość dowolnego punktu z tej paraboli od podanej prostej 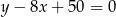y− 8x + 50 = 0 . Korzystamy ze wzoru na odległość punktu od prostej.

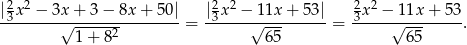
2 2 2 2 2 2 |3x--−-3x√-+-3-−-8x-+--50|= |3x--−√11x-+--53|= 3-x-−-√11x-+-53. 1 + 82 65 65

Wartość bezwzględną mogliśmy opuścić, bo znajdujące się pod nią wyrażanie jest zawsze dodatnie (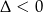Δ < 0 ). No i wszystko wiemy, odległość punktów paraboli od podanej prostej wyraża się funkcją kwadratową, więc przyjmuje najmniejszą wartość w wierzchołku, a na lewo i na prawo od wierzchołka zaczyna rosnąć. Pierwsza współrzędna wierzchołka to

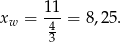
11 xw = 4--= 8,2 5. 3

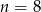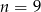No i mamy problem, bo w naszym ciągu nie ma punktu z pierwszą współrzędną równą 8,25. Wiemy jednak, że interesująca nas odległość rośnie gdy oddalamy się od wierzchołka, więc najmniejszą odległość otrzymamy dla n = 8 lub n = 9 . Dla której z tych wartości? Liczymy i sprawdzamy.

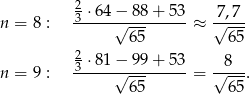
2 n = 8 : 3-⋅64√−-88-+-53-≈ 7√-,7- 6 5 65 2 ⋅81 − 99 + 53 n = 9 : 3----√----------= √-8-. 6 5 65

W zasadzie nie powinno to dziwić, bo 8 jest bliżej wierzchołka niż 9 – jeżeli to zauważymy, to nie trzeba robić powyższego rachunku.  
Odpowiedź: n = 8

Wersja PDF