Zadanie nr 2775700
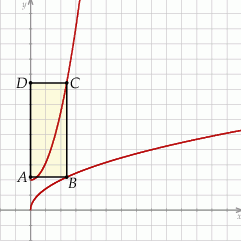
Rozpatrujemy prostokąty 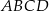 , których dwa wierzchołki leżą na osi
, których dwa wierzchołki leżą na osi 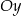 , jeden wierzchołek leży na paraboli określonej równaniem
, jeden wierzchołek leży na paraboli określonej równaniem 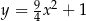 , jeden wierzchołek leży na wykresie funkcji
, jeden wierzchołek leży na wykresie funkcji 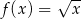 określonej dla
określonej dla 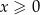 . Oblicz pole tego z tych prostokątów, który ma najmniejszy możliwy obwód.
. Oblicz pole tego z tych prostokątów, który ma najmniejszy możliwy obwód.
Rozwiązanie
Jeżeli przyjmiemy, że 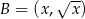 , to
, to 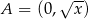 ,
, 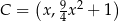 ,
, 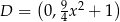 i obwód prostokąta
i obwód prostokąta 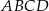 jest równy
jest równy
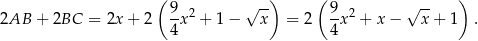
Musimy teraz wyznaczyć wartość najmniejszą funkcji w nawiasie. Aby uniknąć problemów rachunkowych z pierwiastkiem podstawiamy 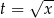 i badamy funkcję
i badamy funkcję
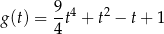
Liczymy pochodną
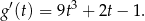
Szukamy teraz miejsc zerowych pochodnej. Dzielniki wyrazu wolnego, czyli 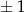 niestety nie są pierwiastkami, więc sprawdzamy ułamki
niestety nie są pierwiastkami, więc sprawdzamy ułamki 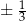 i
i 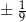 . Gdy to zrobimy okaże się, że jednym z pierwiastków pochodnej jest
. Gdy to zrobimy okaże się, że jednym z pierwiastków pochodnej jest 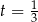 . Dzielimy teraz
. Dzielimy teraz 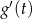 przez
przez 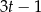 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
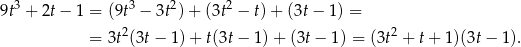
Sprawdzamy teraz, że trójmian w nawiasie jest stale dodatni (bo 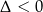 ), więc
), więc 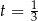 jest jedynym miejscem zerowym pochodnej i pochodna
jest jedynym miejscem zerowym pochodnej i pochodna 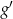 zmienia w tym punkcie znak z ujemnego na dodatni. To oznacza, że funkcja
zmienia w tym punkcie znak z ujemnego na dodatni. To oznacza, że funkcja 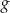 ma w tym punkcie minimum i najmniejszy obwód otrzymamy dla
ma w tym punkcie minimum i najmniejszy obwód otrzymamy dla 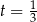 , czyli dla
, czyli dla 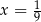 . Pole prostokąta jest wtedy równe
. Pole prostokąta jest wtedy równe
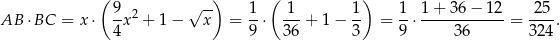
Odpowiedź: