Zadanie nr 4395608
Na paraboli o równaniu 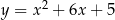 znajdź współrzędne punktu
znajdź współrzędne punktu 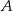 , którego odległość od prostej o równaniu
, którego odległość od prostej o równaniu 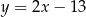 jest najmniejsza.
jest najmniejsza.
Rozwiązanie
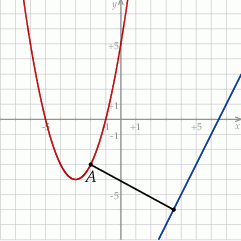
Zacznijmy od szkicowego rysunku i niech 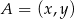 będzie szukanym punktem.
będzie szukanym punktem.
Korzystając ze wzoru na odległość punktu 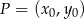 od prostej
od prostej 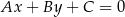 :
:
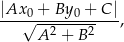
wiemy, że odległość punktu 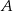 od podanej prostej
od podanej prostej 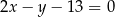 jest równa
jest równa
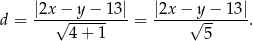
Fajnie byłoby opuścić wartość bezwzględną – aby to zrobić musimy wiedzieć jaki jest znak wyrażenia 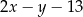 . Z rysunku widzimy, że punkty na paraboli są powyżej danej prostej, tzn. dla takich punktów
. Z rysunku widzimy, że punkty na paraboli są powyżej danej prostej, tzn. dla takich punktów 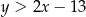 , zatem
, zatem 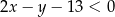 . Opuszczamy więc wartość bezwzględną ze znakiem minus i uwzględniamy równość
. Opuszczamy więc wartość bezwzględną ze znakiem minus i uwzględniamy równość 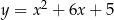 .
.
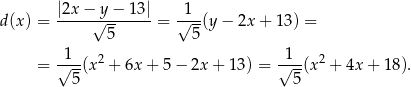
Pozostało wyznaczyć najmniejszą wartość funkcji 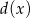 . Wartość ta jest przyjmowana w wierzchołku paraboli, czyli dla
. Wartość ta jest przyjmowana w wierzchołku paraboli, czyli dla 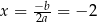 . Wtedy
. Wtedy
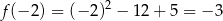
i 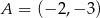 .
.
Odpowiedź: