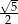Zadanie nr 4478089
Wyznacz te punkty paraboli 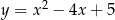 , które znajdują się najbliżej punktu
, które znajdują się najbliżej punktu 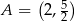 . Oblicz tę najmniejszą odległość.
. Oblicz tę najmniejszą odległość.
Rozwiązanie
Dana parabola
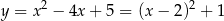
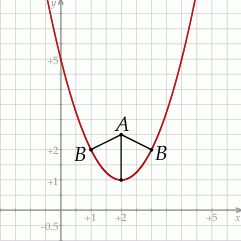
to parabola o ramionach skierowanych w górę i wierzchołku w punkcie 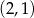 . Szkicujemy tę sytuację.
. Szkicujemy tę sytuację.
Jeżeli 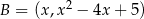 jest dowolnym punktem paraboli, to
jest dowolnym punktem paraboli, to
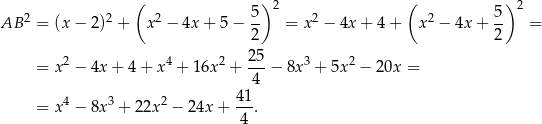
Po drodze skorzystaliśmy ze wzoru skróconego mnożenia
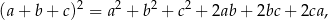
ale oczywiście nie było to konieczne – mogliśmy po prostu wymnożyć dwa nawiasy. Musimy teraz zbadać otrzymaną funkcję – liczymy jej pochodną
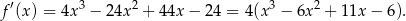
Łatwo zauważyć, że jednym z miejsc zerowych pochodnej jest 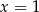 , więc dzielimy wielomian w nawiasie przez
, więc dzielimy wielomian w nawiasie przez 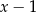 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
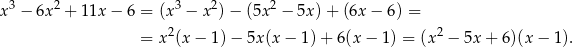
Rozkładamy jeszcze trójmian w nawiasie.
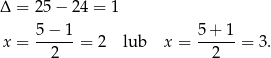
W takim razie
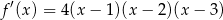
i pochodna w punktach 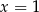 i
i 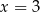 zmienia znak z ujemnego na dodatni, a w punkcie
zmienia znak z ujemnego na dodatni, a w punkcie 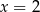 zmienia znak z dodatniego na ujemny. W takim razie w punktach
zmienia znak z dodatniego na ujemny. W takim razie w punktach 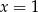 i
i 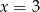 funkcja
funkcja 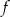 ma minima lokalne i dla jednej z tych wartości (lub dla obu) otrzymamy najkrótszą długość odcinka
ma minima lokalne i dla jednej z tych wartości (lub dla obu) otrzymamy najkrótszą długość odcinka 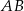 . Liczymy
. Liczymy
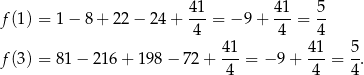
Są więc dwa punkty spełniające warunki zadania: 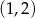 i
i 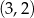 .
.
Odpowiedź: 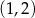 i
i 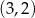 , min. odległość:
, min. odległość: