Zadanie nr 7161386
Na obrzeżach miasta znajduje się jezioro, na którym postanowiono stworzyć tor regatowy. Na podstawie dostępnych map wymodelowano w pewnej skali kształt linii brzegowej jeziora w kartezjańskim układzie współrzędnych 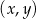 za pomocą fragmentów wykresów funkcji
za pomocą fragmentów wykresów funkcji 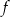 oraz
oraz 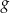 (zobacz rysunek).
(zobacz rysunek).
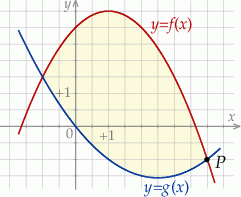
Funkcje 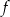 oraz
oraz 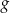 są określone wzorami
są określone wzorami 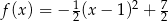 oraz
oraz 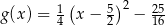 . Początek toru postanowiono zlokalizować na brzegu w miejscu, któremu odpowiada w układzie współrzędnych punkt
. Początek toru postanowiono zlokalizować na brzegu w miejscu, któremu odpowiada w układzie współrzędnych punkt 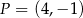 . Koniec toru regatowego należy umieścić na linii brzegowej. Oblicz współrzędne punktu
. Koniec toru regatowego należy umieścić na linii brzegowej. Oblicz współrzędne punktu 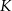 , w którym należy zlokalizować koniec toru, aby długość toru (tj. odległość końca
, w którym należy zlokalizować koniec toru, aby długość toru (tj. odległość końca 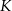 toru od początku
toru od początku 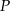 ) była możliwie największa. Oblicz długość najdłuższego toru.
) była możliwie największa. Oblicz długość najdłuższego toru.
Przy rozwiązywaniu zadania możesz skorzystać z tego, że odległość dowolnego punktu 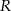 leżącego na wykresie funkcji
leżącego na wykresie funkcji 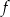 od punktu
od punktu 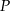 wyraża się wzorem
wyraża się wzorem
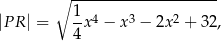
gdzie  jest pierwszą współrzędną punktu
jest pierwszą współrzędną punktu 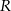 .
.

