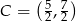Zadanie nr 6469111
Na prostej 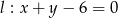 wyznacz taki punkt
wyznacz taki punkt 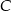 , aby długość łamanej
, aby długość łamanej 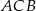 , gdzie
, gdzie 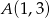 ,
, 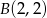 , była najmniejsza. Uzasadnij swoje rozumowanie.
, była najmniejsza. Uzasadnij swoje rozumowanie.
Rozwiązanie
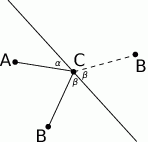
Zacznijmy od szkicowego rysunku.
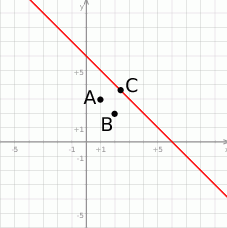
Rysunek sugeruje nam, że punkty  i
i 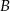 są w tej samej odległości od prostej
są w tej samej odległości od prostej 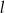 . Sprawdźmy, że tak jest w istocie. Korzystamy ze wzoru na odległość punktu
. Sprawdźmy, że tak jest w istocie. Korzystamy ze wzoru na odległość punktu 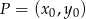 od prostej
od prostej 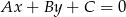 :
:
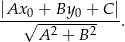
W naszej sytuacji
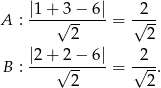
Teraz skorzystamy z faktu, że jeżeli mamy dwa punkty 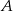 i
i 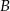 po jednej stronie prostej, to punkt
po jednej stronie prostej, to punkt 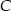 na tej prostej, dla którego łamana
na tej prostej, dla którego łamana 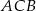 jest najkrótsza to punkt, dla którego kąty jakie tworzą odcinki
jest najkrótsza to punkt, dla którego kąty jakie tworzą odcinki 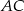 i
i 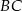 z daną prostą są równe (rysunek).
z daną prostą są równe (rysunek).
Uzasadnienie tego jest proste, jeżeli 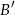 jest obrazem punktu
jest obrazem punktu 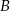 w symetrii względem danej prostej, to
w symetrii względem danej prostej, to
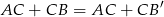
i ta ostatnia liczba jest najmniejsza, gdy punkty 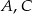 i
i 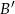 leżą na jednej prostej, co sprowadza się do warunku
leżą na jednej prostej, co sprowadza się do warunku 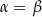 .
.
W sytuacji naszego zadania, sprawa jest wyjątkowo prosta, bo punkty leżą w jednakowej odległości od prostej 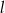 . W takiej sytuacji, warunek z kątami oznacza, że punkt
. W takiej sytuacji, warunek z kątami oznacza, że punkt 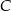 leży na symetralnej odcinka
leży na symetralnej odcinka 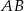 . Wyliczmy jej równanie. Będziemy korzystać ze wzoru na równanie prostej prostopadłej do wektora
. Wyliczmy jej równanie. Będziemy korzystać ze wzoru na równanie prostej prostopadłej do wektora ![→ v = [p,q]](https://img.zadania.info/zad/6469111/HzadR24x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 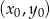
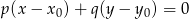
W naszej sytuacji ![→ → v = AB = [1,− 1]](https://img.zadania.info/zad/6469111/HzadR27x.gif) i
i 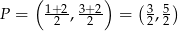 . Mamy zatem równanie symetralnej
. Mamy zatem równanie symetralnej
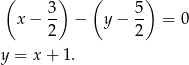
Pozostało znaleźć punkt przecięcia się tej prostej z prostą 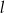
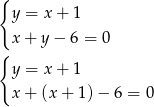
Łatwo stąd wyliczyć, że 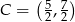 .
.
Odpowiedź: