/Szkoła średnia/Geometria/Stereometria/Graniastosłup

Zadanie nr 1899922

Dodaj do ulubionych
Dodaj do rozwiązanych

Objętość graniastosłupa prawidłowego trójkątnego jest równa 8, a przekątne dwóch ścian bocznych poprowadzone z jednego wierzchołka tworzą kąt α . Oblicz długość krawędzi podstawy tego graniastosłupa.

Rozwiązanie

Oznaczmy przez 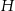H i a długości odpowiednio wysokości i krawędzi podstawy graniastosłupa.

PIC

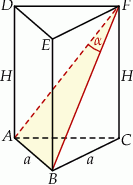
Podana objętość pozwala powiązać a z H .

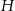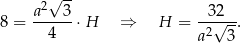
2√ -- 8 = a---3-⋅H ⇒ H = -32√--. 4 a2 3

Piszemy teraz twierdzenie Pitagorasa w trójkącie 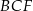BCF .

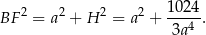
2 2 2 2 1024- BF = a + H = a + 3a4 .

Sposób I

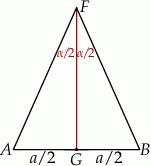
Piszemy twierdzenie cosinusów w trójkącie 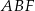ABF .

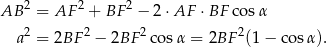
2 2 2 AB = AF + BF − 2⋅AF ⋅BF co sα a2 = 2BF 2 − 2BF 2cos α = 2BF 2(1 − cos α).

Podstawiamy obliczone wcześniej 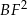BF 2 .

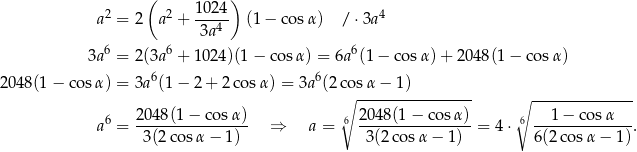
( 1024) a2 = 2 a2 + ---4- (1− cosα) / ⋅3a4 3a 3a6 = 2(3a 6 + 1 024)(1 − cos α) = 6a6(1 − cos α)+ 2048(1 − co sα) 6 6 2048(1 − co sα) = 3a (1− 2 + 2 cos α) = 3a (2 cosα − 1) ∘ ---------------- ∘ -------------- a6 = 2048(1-−-cos-α)- ⇒ a = 6 204-8(1−--cosα-)= 4 ⋅ 6---1−--cosα---. 3(2cos α− 1) 3(2 cosα − 1 ) 6(2 cos α− 1)

Sposób II

Tym razem dorysujmy wysokość 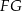F G trójkąta ABF .

PIC

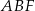W trójkącie prostokątnym 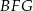BF G mamy

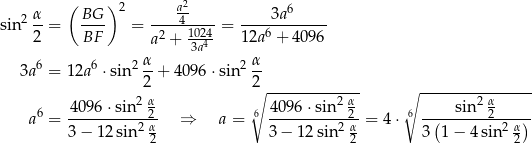
( ) 2 a2 6 sin2 α-= BG-- = ----4---- = -----3a----- 2 BF a2 + 10244 1 2a6 + 4096 α 3a α 3a6 = 12a6 ⋅ sin2--+ 40 96⋅ sin2 -- 2 2∘ ------------- ∘ ---------------- 4096 ⋅sin2 α 4096 ⋅sin 2 α sin2 α a6 = ---------2-2α- ⇒ a = 6 ----------22α = 4 ⋅ 6--(-------22-α) 3− 12sin 2 3 − 12 sin 2 3 1 − 4 sin 2

 
Odpowiedź: ∘ ---------- ∘ ----sin2 α--- 4 ⋅ 6 6(12−ccoossαα−1) = 4 ⋅ 6------22 α- 3(1− 4sin 2)

Wersja PDF