Zadanie nr 3074365

Podstawą prostopadłościanu jest kwadrat o boku długości 4, a wysokość prostopadłościanu jest równa 8. Połączono odcinkami środki trzech krawędzi prostopadłościanu, z których żadne dwie nie leżą w jednej płaszczyźnie, i otrzymano trójkąt 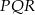PQR

Oblicz długości boków trójkąta .
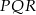Wyznacz miary kątów trójkąta .

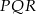Rozwiązanie

Zaczynamy oczywiście od rysunku.

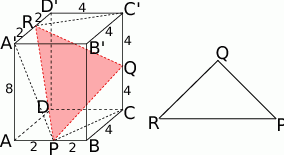
Aby wyliczyć szukane długości boków, wyliczymy najpierw (z twierdzenia Pitagorasa) długości odcinków 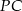, 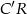i .

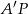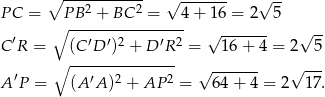
$∘ ----------- √ ------- √ -- P C = PB 2 + BC 2 = 4 + 16 = 2 5 ∘ ---------------- √ ------- √ -- C ′R = (C′D ′)2 + D ′R2 = 16+ 4 = 2 5 ∘ --------------- √ ------- √ --- A ′P = (A ′A )2 + AP 2 = 64 + 4 = 2 17.$

Liczymy teraz szukane boki

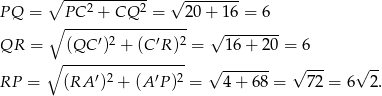
$------------ P Q = ∘ P C2 + CQ 2 = √ 20+--16-= 6 ∘ ----------------- QR = (QC ′)2 + (C ′R )2 = √ 16-+-20-= 6 ∘ ----------------- ′ 2 ′ 2 √ ------- √ --- √ -- RP = (RA ) + (A P ) = 4 + 68 = 7 2 = 6 2.$

Odpowiedź: 6,6 i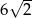
Ponieważ trójkąt 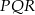jest równoramienny i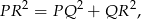
$2 2 2 PR = P Q + QR ,$

jest to równoramienny trójkąt prostokątny (połówka kwadratu). Zatem jego kąty wynoszą 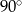, 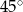i .
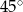Odpowiedź: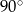 , 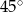i