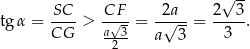/Szkoła średnia/Geometria/Stereometria/Graniastosłup

Zadanie nr 3343080

Dodaj do ulubionych
Dodaj do rozwiązanych

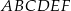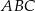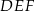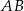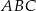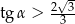Dany jest graniastosłup prawidłowy trójkątny ABCDEF o podstawach ABC i DEF , w którym wszystkie krawędzie mają tę samą długość. Wykaż, że jeżeli przekrój tego graniastosłupa płaszczyzną zawierającą krawędź podstawy AB jest trapezem, to płaszczyzna ta jest nachylona do płaszczyzny podstawy ABC tego graniastosłupa pod takim kątem α , że √- tg α > 233- .

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

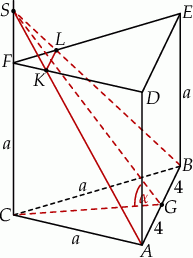
Niech 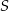S będzie punktem wspólnym danej płaszczyzny przekroju oraz prostej 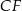CF . Zauważmy, że jeżeli 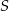S jest punktem odcinka 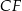CF , to przekrój jest trójkątem, więc punkt 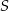S musi leżeć po drugiej stronie punktu 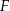F , niż punkt 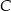C . Jest to też oczywiście warunek wystarczający, więc przekrój jest trapezem wtedy i tylko wtedy, gdy SC > CF .

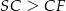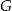Jeżeli oznaczymy długość każdej krawędzi graniastosłupa przez a i G jest środkiem krawędzi 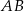AB , to

√ -- SC-- CF-- -2a-- 2--3- tgα = CG > a√3-= √ --= 3 . 2 a 3
Wersja PDF