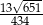Zadanie nr 3905626
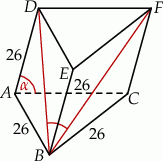
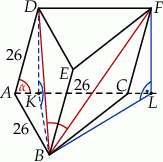
Każda krawędź graniastosłupa trójkątnego ma długość 26. Ściana boczna 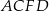 jest prostopadła do płaszczyzny podstawy
jest prostopadła do płaszczyzny podstawy  , a krawędź
, a krawędź  jest nachylona do płaszczyzny podstawy pod katem
jest nachylona do płaszczyzny podstawy pod katem  takim, że
takim, że 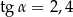 (zobacz rysunek).
(zobacz rysunek).
Oblicz cosinus kąta 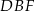 .
.
Rozwiązanie
Dorysujmy rzuty 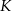 i
i  punktów
punktów  i
i  na płaszczyznę podstawy.
na płaszczyznę podstawy.
Ponieważ płaszczyzny 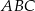 i
i 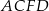 są prostopadłe, punkty
są prostopadłe, punkty 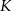 i
i 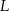 leżą na prostej
leżą na prostej 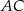 oraz każdy z trójkątów
oraz każdy z trójkątów 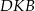 i
i 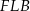 jest prostokątny. Właśnie te trójkąty pozwolą nam obliczyć długości odcinków
jest prostokątny. Właśnie te trójkąty pozwolą nam obliczyć długości odcinków 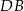 i
i  . Zanim jednak to zrobimy obliczmy pozostałe funkcje trygonometryczne kąta
. Zanim jednak to zrobimy obliczmy pozostałe funkcje trygonometryczne kąta  .
.
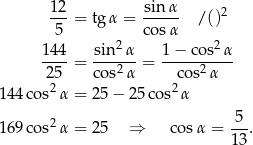
Stąd
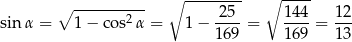
oraz
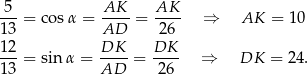
Teraz obliczymy długość odcinka 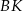 – korzystamy z twierdzenia cosinusów w trójkącie
– korzystamy z twierdzenia cosinusów w trójkącie 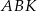 (trójkąt
(trójkąt 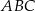 jest równoboczny, więc
jest równoboczny, więc 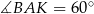 ).
).
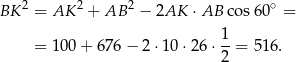
Stąd
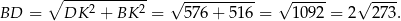
W podobny sposób obliczymy długość odcinka 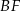 . Zauważmy najpierw, że trójkąty
. Zauważmy najpierw, że trójkąty 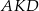 i
i 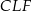 są przystające, więc
są przystające, więc 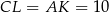 ,
, 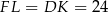 . Piszemy teraz twierdzenie cosinusów w trójkącie
. Piszemy teraz twierdzenie cosinusów w trójkącie 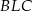 .
.
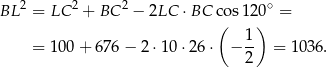
Stąd
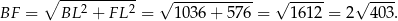
Pozostało teraz napisać twierdzenie cosinusów w trójkącie  .
.
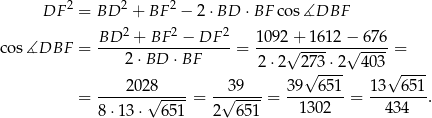
Odpowiedź: