/Szkoła średnia/Geometria/Stereometria/Graniastosłup

Zadanie nr 4742975

Dodaj do ulubionych
Dodaj do rozwiązanych

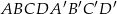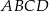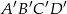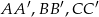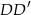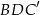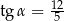Dany jest graniastosłup prawidłowy czworokątny ′ ′ ′ ′ ABCDA B C D o podstawach ABCD i A ′B ′C ′D ′ , oraz krawędziach bocznych AA ′,BB ′,CC ′ i DD ′ . Oblicz pole trójkąta BDC ′ wiedząc, że przekątna ściany bocznej ma długość 13 i jest nachylona do podstawy pod takim kątem α , że 12 tg α = 5 .

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

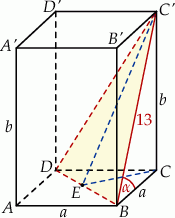
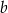Z podanego tangensa i długości przekątnej ściany obliczymy długości krawędzi a i b graniastosłupa. Na mocy twierdzenia Pitagorasa w trójkącie 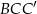BCC ′ mamy

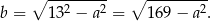
∘ --------- ∘ --------- b = 132 − a2 = 169 − a2.

Teraz korzystamy z podanego tangensa.

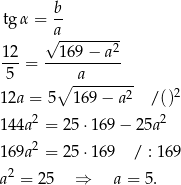
b- tgα = a √ -------2- 12-= --169-−-a-- 5 ∘ -a------- 1 2a = 5 1 69− a2 / ()2 1 44a2 = 25 ⋅169 − 25a 2 2 1 69a = 25 ⋅169 / : 169 a 2 = 25 ⇒ a = 5 .

Zatem 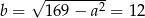√ --------2 b = 16 9− a = 12 .

Znamy więc długość podstawy trójkąta równoramiennego 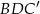′ BDC :

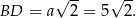
√ -- √ -- BD = a 2 = 5 2.

Wysokość tego trójkąta obliczamy patrząc na trójkąt prostokątny 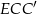′ ECC .

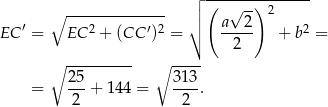
┌│ (--√--)-2------ ′ ∘ -------------- │∘ a 2 EC = EC 2 + (CC ′)2 = ----- + b2 = 2 ∘ --------- ∘ ---- = 25-+ 144 = 31-3. 2 2

Zatem interesujące nas pole trójkąta 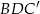′ BDC jest równe

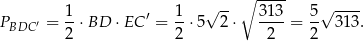
-- ∘ ---- ---- P ′ = 1-⋅BD ⋅EC ′ = 1-⋅5√ 2 ⋅ 313-= 5√ 313. BDC 2 2 2 2

 
Odpowiedź: √ ---- 5 3 13 2

Wersja PDF