/Szkoła średnia/Geometria/Stereometria/Graniastosłup

Zadanie nr 6293889

Dodaj do ulubionych
Dodaj do rozwiązanych

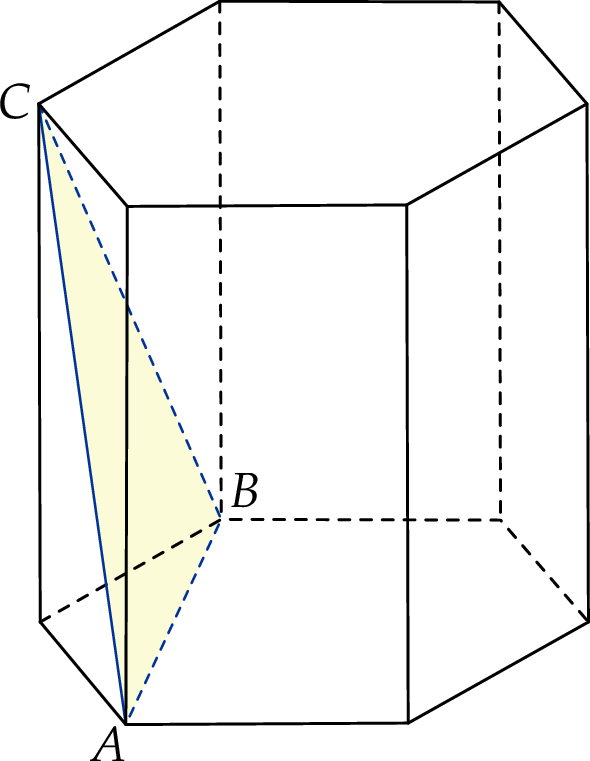
W graniastosłupie prawidłowym sześciokątnym płaszczyzna 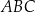ABC zawierająca przekątne sąsiednich ścian bocznych, wychodzących z tego samego wierzchołka, jest nachylona do podstawy graniastosłupa pod kątem 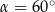α = 60∘ . Pole przekroju graniastosłupa tą płaszczyzną równa się 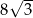8√ 3- . Zaznacz na poniższym rysunku kąt α . Oblicz objętość tego graniastosłupa.

ZINFO-FIGURE

Rozwiązanie

Zacznijmy od zaznaczenia podanego kąta.

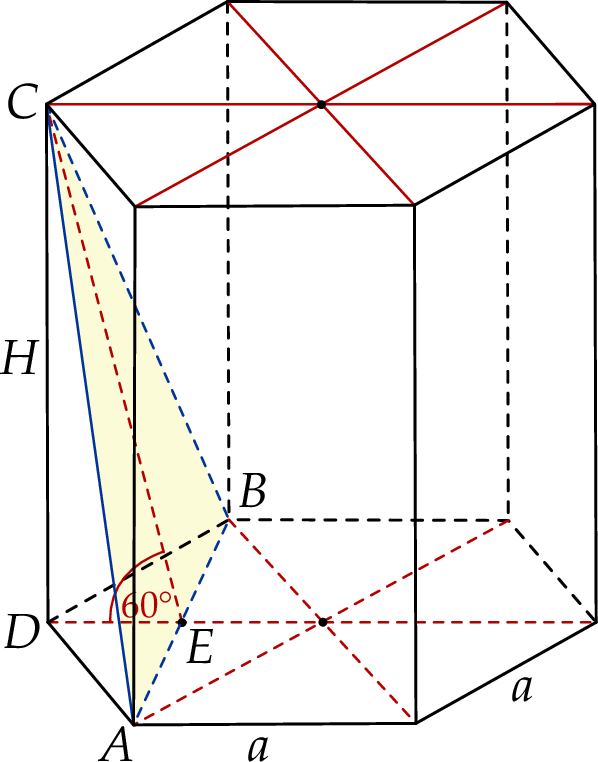
ZINFO-FIGURE

Aby obliczyć objętość graniastosłupa potrzebujemy znać jego wysokość 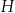H i pole podstawy. Podstawa składa się z 6 trójkątów równobocznych, oznaczmy długość ich boku przez a . Spróbujmy najpierw jakoś wykorzystać podaną informację o polu trójkąta 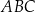ABC . W tym celu wyrazimy to pole w zależności od a i H .

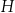Zauważmy, że odcinek 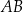AB jest dwa razy dłuższy niż wysokość trójkątów równobocznych, które są w podstawie. Zatem (ze wzoru na wysokość w trójkącie równobocznym a√-3 h = 2 )

√ -- AB = a 3.

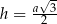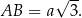
Natomiast wysykość 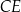CE trójkąta 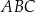ABC obliczamy z trójkąta prostokątnego CDE :

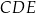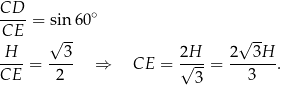
CD-- ∘ CE = sin 60 √ -- √ -- H---= --3- ⇒ CE = 2√H--= 2---3H-. CE 2 3 3

Możemy zatem zapisać warunek z polem:

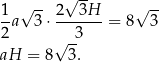
√ -- 1- √ -- 2--3H-- √ -- 2 a 3⋅ 3 = 8 3 √ -- aH = 8 3.

Skąd wziąć jeszcze jedno równanie? – jeszcze raz korzystamy z trójkąta 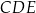CDE oraz z faktu, że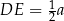 DE = 12a

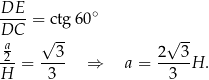
DE--= ctg 60∘ DC a √ 3- 2 √ 3- 2- = ---- ⇒ a = -----H . H 3 3

Z obu otrzymanych związków dostajemy

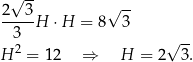
√ -- √ -- 2--3H ⋅H = 8 3 3 √ -- H 2 = 12 ⇒ H = 2 3.

Stąd

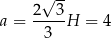
2√ 3- a = ----H = 4 3

Teraz bez problemu liczymy objętość (korzystamy ze wzoru na pole trójkąta równobocznego 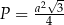2√- P = a--3 4 )

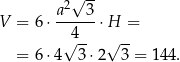
√ -- a2 3 V = 6 ⋅------⋅H = √4-- √ -- = 6 ⋅4 3 ⋅2 3 = 144.

 
Odpowiedź: 144

Wersja PDF