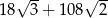Zadanie nr 6374980

W graniastosłupie prawidłowym trójkątnym o krawędzi podstawy 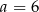a = 6 przekątna ściany bocznej tworzy z drugą ścianą boczną kąt o mierze 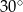30 ∘ . Oblicz

długość przekątnej ściany bocznej,
długość wysokości graniastosłupa,
objętość i pole powierzchni całkowitej.

Rozwiązanie

Zacznijmy od rysunku.

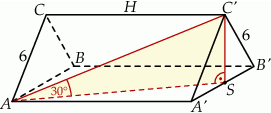
Rysunek specjalnie narysowaliśmy trochę nietypowo (graniastosłup leży na ścianie bocznej) — dzięki temu lepiej widać jak wygląda rzut przekątnej ściany bocznej na sąsiednią ścianę, w szczególności widać, że rzut 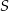wierzchołka 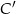to środek krawędzi ′ ′ A B .

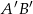Z trójkąta prostokątnego 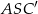mamy
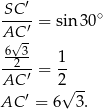
$′ SC---= sin3 0∘ AC√-′ 6-3- -2---= 1- AC ′ 2√ -- AC ′ = 6 3.$

W powyższych rachunkach skorzystaliśmy ze wzoru na wysokość w trójkącie równobocznym .
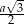Odpowiedź: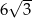
Wysokość 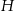liczymy z trójkąta prostokatnego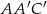
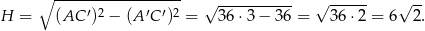
$∘ ------------------ H = (AC ′)2 − (A′C ′)2 = √ 3-6⋅3-−-36-= √ 36⋅-2 = 6√ 2.$

Odpowiedź: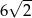
Najpierw liczymy objętość
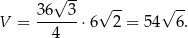
$√ -- √ -- √ -- V = 36--3-⋅6 2 = 54 6. 4$

Pole powierzchni

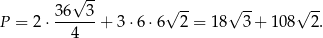
$36√ 3- √ -- √ -- √ -- P = 2 ⋅------+ 3 ⋅6 ⋅6 2 = 1 8 3+ 108 2. 4$

Korzystaliśmy powyżej ze wzoru na pole trójkąta równobocznego .
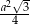Odpowiedź: Objętość: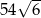 , pole powierzchni: