/Szkoła średnia/Geometria/Stereometria/Graniastosłup

Zadanie nr 6805882

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą prostopadłościanu jest kwadrat. Przekątna tego prostopadłościanu ma długość 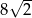√ -- 8 2 i jest nachylona do płaszczyzny podstawy pod kątem 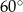60 ∘ . Oblicz objętość i pole powierzchni całkowitej prostopadłościanu i wykonaj rysunek.

Rozwiązanie

Zaczynamy od rysunku.

PIC

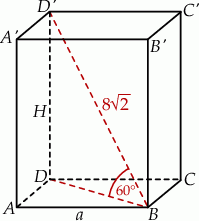
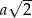Ponieważ przekątna kwadratu o boku a ma długość √ -- a 2 , patrząc na trójkąt prostokątny 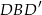DBD ′ , mamy równanie

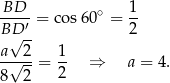
-BD--= cos6 0∘ = 1- BD ′- 2 a√ 2 1 -√----= -- ⇒ a = 4. 8 2 2

Podobnie obliczamy wysokość 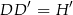DD ′ = H ′ .

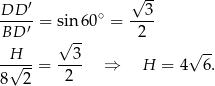
′ √ -- DD--- = sin6 0∘ = --3- BD ′ -- 2 H √ 3 √ -- -√---= ---- ⇒ H = 4 6. 8 2 2

Możemy teraz obliczyć objętość i pole powierzchni całkowitej.

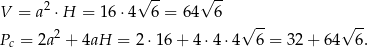
2 √ -- √ -- V = a ⋅H = 1 6⋅4 6 = 64 6 -- -- P = 2a2 + 4aH = 2 ⋅16 + 4 ⋅4 ⋅4√ 6 = 32 + 64 √ 6. c

 
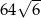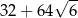Odpowiedź: Objętość: √ -- 6 4 6 , pole powierzchni: √ -- 32 + 64 6 .

Wersja PDF