/Szkoła średnia/Geometria/Stereometria/Graniastosłup

Zadanie nr 8278749

Dodaj do ulubionych
Dodaj do rozwiązanych

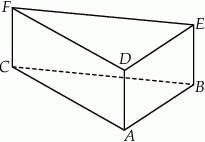
Dany jest graniastosłup prawidłowy trójkątny (zobacz rysunek). Pole powierzchni całkowitej tego graniastosłupa jest równe 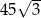√ -- 45 3 . Pole podstawy graniastosłupa jest równe polu jednej ściany bocznej. Oblicz objętość tego graniastosłupa.

PIC

Rozwiązanie

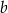Oznaczmy przez a długość krawędzi podstawy graniastosłupa, a przez b długość jego krawędzi bocznej. W takim razie pole podstawy jest równe

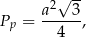
√ -- a2--3- Pp = 4 ,

a pole jednej ściany bocznej jest równe

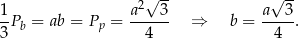
√ -- √ -- 1- a-2--3 a--3- 3Pb = ab = Pp = 4 ⇒ b = 4 .

Korzystamy teraz z podanej informacji o polu powierzchni całkowitej graniastosłupa

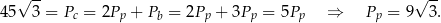
√ -- √ -- 45 3 = Pc = 2Pp + Pb = 2Pp + 3Pp = 5Pp ⇒ Pp = 9 3.

Stąd

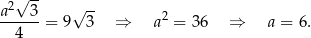
√ -- a2--3- √ -- 2 4 = 9 3 ⇒ a = 36 ⇒ a = 6.

Zatem

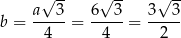
√ -- √ -- √ -- b = a--3-= 6--3-= 3--3- 4 4 2

i objętość graniastosłupa jest równa

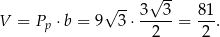
√ -- V = P ⋅b = 9√ 3-⋅ 3-3-= 81-. p 2 2

 
Odpowiedź: V = 81 2

Wersja PDF