/Szkoła średnia/Geometria/Stereometria/Graniastosłup

Zadanie nr 8953864

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą graniastosłupa prostego 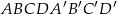′ ′ ′ ′ ABCDA B C D jest romb 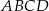ABCD . Przekątna 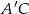A ′C tego graniastosłupa ma długość 6 i jest nachylona do płaszczyzny podstawy pod kątem 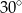3 0∘ , a objętość graniastosłupa jest równa 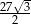27√-3- 2 . Oblicz pole powierzchni całkowitej tego graniastosłupa.

PIC

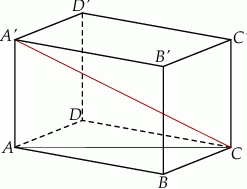
Rozwiązanie

Patrzymy najpierw na trójkąt prostokątny 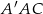′ A AC . Mamy w nim

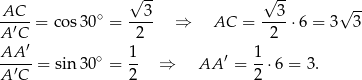
√ -- √ -- √ -- AC---= cos30 ∘ = --3- ⇒ AC = --3-⋅6 = 3 3 A ′C 2 2 AA--′ ∘ 1- ′ 1- A ′C = sin 30 = 2 ⇒ AA = 2 ⋅6 = 3 .

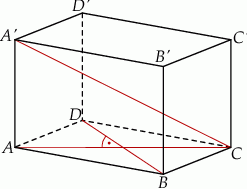
Dorysujmy drugą przekątną w podstawie graniastosłupa.

PIC

Jeżeli oznaczymy 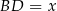BD = x , to

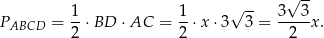
√ -- P = 1⋅BD ⋅ AC = 1-⋅x ⋅3√ 3-= 3--3x . ABCD 2 2 2

Korzystamy teraz z podanej objętości graniastosłupa.

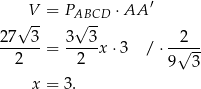
′ V--= PABCD ⋅AA 27√ 3 3√ 3 2 ------ = -----x ⋅3 / ⋅--√--- 2 2 9 3 x = 3.

Pole rombu w podstawie jest więc równe

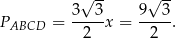
√ -- √ -- 3 3 9 3 PABCD = ----x = -----. 2 2

Teraz z trójkąta prostokątnego w podstawie graniastosłupa obliczamy długość krawędzi podstawy.

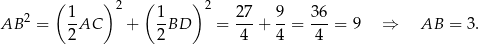
( ) 2 ( ) 2 AB 2 = 1-AC + 1BD = 2-7+ 9-= 36-= 9 ⇒ AB = 3. 2 2 4 4 4

Pole powierzchni bocznej jest więc równe

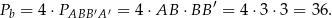
′ Pb = 4 ⋅PABB ′A′ = 4⋅AB ⋅BB = 4 ⋅3 ⋅3 = 36.

Pole powierzchni całkowitej jest więc równe

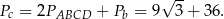
√ -- Pc = 2PABCD + Pb = 9 3+ 36.

 
Odpowiedź: √ -- Pc = 9 3+ 36

Wersja PDF