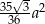/Szkoła średnia/Geometria/Stereometria/Graniastosłup

Zadanie nr 9678897

Dodaj do ulubionych
Dodaj do rozwiązanych

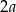Dany jest graniastosłup prawidłowy trójkątny o krawędzi podstawy a i wysokości 2a . Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź dolnej podstawy i środek ciężkości górnej podstawy. Oblicz pole otrzymanego przekroju.

Rozwiązanie

Zaczynamy oczywiście od dużego rysunku.

PIC

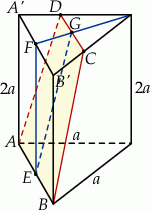
Przedmiotowy przekrój jest trapezem równoramiennym o jednej z podstaw długości a . Aby obliczyć pole tego przekroju musimy wyznaczyć długość drugiej podstawy i wysokość trapezu.

Z drugą podstawą jest łatwo, ponieważ środek ciężkości dzieli wysokość w stosunku 2:1,

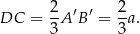
2 2 DC = --A′B ′ = -a. 3 3

Wysokość możemy wyliczyć z trójkąta prostokątnego 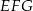EF G .

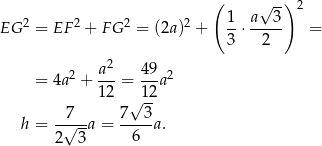
( √ --) 2 EG 2 = EF 2 + FG 2 = (2a)2 + 1-⋅ a-3- = 3 2 2 a-2 49- 2 = 4a + 12 = 12 a √ -- h = -√7--a = 7---3a. 2 3 6

Stąd pole

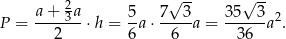
2 √ -- √ -- a-+-3a- 5- 7--3- 35---3 2 P = 2 ⋅h = 6a ⋅ 6 a = 36 a .

 
Odpowiedź: √ - 35--3a2 36

Wersja PDF