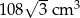Zadanie nr 9735732
W graniastosłupie prostym o podstawie rombu krótsza przekątna podstawy ma długość 6 cm i tworzy z krawędzią podstawy kąt 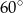 . Kąt między krótszą przekątną rombu i krótszą przekątną graniastosłupa ma miarę
. Kąt między krótszą przekątną rombu i krótszą przekątną graniastosłupa ma miarę 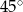 . Oblicz objętość graniastosłupa.
. Oblicz objętość graniastosłupa.
Rozwiązanie
Szkicujemy graniastosłup.
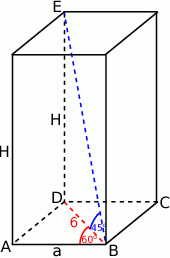
Zauważmy, że trójkąt 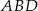 jest równoramienny (
jest równoramienny (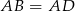 ) z jednym kątem
) z jednym kątem 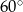 . Musi to więc być trójkąt równoboczny. Zatem
. Musi to więc być trójkąt równoboczny. Zatem 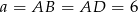 i pole podstawy graniastosłupa jest równe
i pole podstawy graniastosłupa jest równe
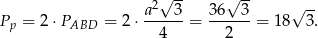
Aby obliczyć wysokość 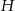 graniastosłupa patrzymy na trójkąt prostokątny
graniastosłupa patrzymy na trójkąt prostokątny 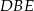 .
.
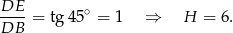
Liczymy objętość graniastosłupa.
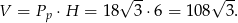
Odpowiedź: