Zadanie nr 8972309
Wykres funkcji kwadratowej 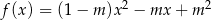 przecina oś
przecina oś 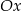 w punktach
w punktach 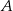 i
i 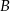 , które leżą po dwóch różnych stronach osi
, które leżą po dwóch różnych stronach osi 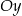 . Wyznacz tę wartość parametru
. Wyznacz tę wartość parametru 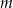 , dla której iloczyn odległości punktów
, dla której iloczyn odległości punktów 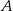 i
i 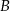 od początku układu współrzędnych jest najmniejszy możliwy. Dla wyznaczonej wartości
od początku układu współrzędnych jest najmniejszy możliwy. Dla wyznaczonej wartości 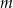 oblicz sumę odległości punktów
oblicz sumę odległości punktów 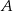 i
i 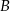 od początku układu współrzędnych.
od początku układu współrzędnych.
Rozwiązanie
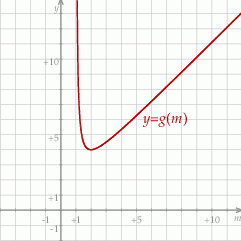
Naszkicujmy opisaną sytuację.
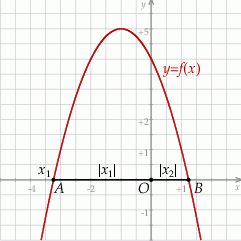
Sprawdźmy najpierw, kiedy funkcja 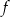 ma dwa miejsca zerowe. Oczywiście musi być
ma dwa miejsca zerowe. Oczywiście musi być 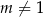 oraz
oraz
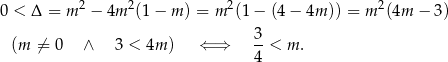
Równanie ma więc dwa różne rozwiązania dla
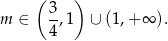
Przy tym założeniu możemy zapisać wzory Viète’a.
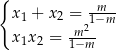
Zauważmy teraz, że informacja o tym, że miejsca zerowe funkcji 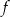 znajdują się po dwóch różnych stronach osi
znajdują się po dwóch różnych stronach osi 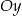 oznacza, że
oznacza, że 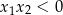 , czyli
, czyli
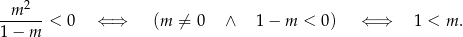
Pozostaje wyznaczyć najmniejszą wartość funkcji
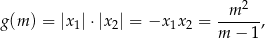
określonej dla 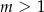 .
.
Liczymy pochodną
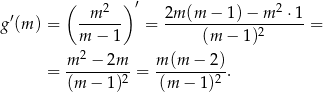
Widać teraz, że pochodna jest ujemna na przedziale 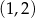 i dodatnia na przedziale
i dodatnia na przedziale 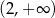 . To oznacza, że funkcja
. To oznacza, że funkcja 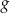 maleje na przedziale
maleje na przedziale 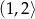 i rośnie na przedziale
i rośnie na przedziale 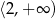 . To z kolei oznacza, że w
. To z kolei oznacza, że w 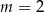 funkcja
funkcja 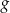 ma minimum lokalne, które jednocześnie jest najmniejszą wartością funkcji.
ma minimum lokalne, które jednocześnie jest najmniejszą wartością funkcji.
Pozostało teraz obliczyć sumę odległości punktów 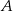 i
i 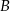 od początku układu współrzędnych. W tym miejscu łatwo popełnić błąd – bo nie jest to suma
od początku układu współrzędnych. W tym miejscu łatwo popełnić błąd – bo nie jest to suma 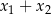 , tylko
, tylko 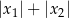 . Obliczymy tę sumę na dwa sposoby.
. Obliczymy tę sumę na dwa sposoby.
Sposób I
Na mocy wzorów Viète’a mamy
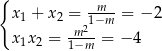
Wiemy, że pierwiastki są różnych znaków, więc możemy założyć, że 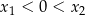 . Mamy wtedy
. Mamy wtedy
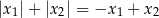
i
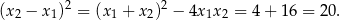
Stąd
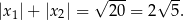
Sposób II
Wyznaczmy pierwiastki funkcji 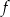 dla
dla 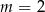 .
.
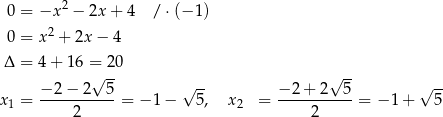
Mamy stąd
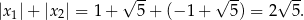
Odpowiedź: 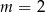 ,
,