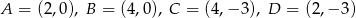Zadanie nr 6487887
Rozważamy prostokąty, których dwa wierzchołki leżą na odcinku łączącym punkty wspólne osi 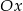 i paraboli o równaniu
i paraboli o równaniu 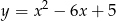 , a dwa należą do tej paraboli. Wyznacz współrzędne wierzchołków tego prostokąta, który ma największy obwód.
, a dwa należą do tej paraboli. Wyznacz współrzędne wierzchołków tego prostokąta, który ma największy obwód.
Rozwiązanie
Zacznijmy od szkicowego rysunku.
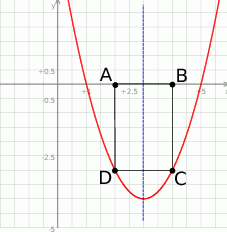
Jeżeli oznaczymy współrzędne punktu 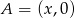 , to punkt
, to punkt 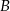 musi być symetryczny względem pionowej prostej przechodzącej przez wierzchołek paraboli. Ponieważ
musi być symetryczny względem pionowej prostej przechodzącej przez wierzchołek paraboli. Ponieważ
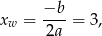
Więc jeżeli 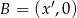 , to
, to 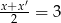 , czyli
, czyli 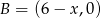 . Łatwo wtedy wyliczyć współrzędne pozostałych wierzchołków
. Łatwo wtedy wyliczyć współrzędne pozostałych wierzchołków
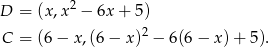
Obwód prostokąta wyraża się wzorem
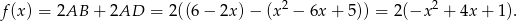
Musimy znaleźć największą wartość funkcji 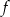 na przedziale
na przedziale 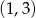 . Ponieważ wykresem tej funkcji jest parabola o ramionach skierowanych w dół, więc największa wartość jest przyjmowana w wierzchołku, czyli dla
. Ponieważ wykresem tej funkcji jest parabola o ramionach skierowanych w dół, więc największa wartość jest przyjmowana w wierzchołku, czyli dla 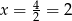 . Wtedy
. Wtedy
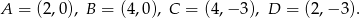
Odpowiedź: