/Szkoła średnia/Zadania testowe/Równania/Układy równań/Dany układ/Liniowy

Zadanie nr 1891167

Na jednym z poniższych rysunków przedstawiono interpretację geometryczną układu równań 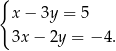{ x− 3y = 5 3x− 2y = − 4. Wskaż ten rysunek:

PIC

Wersja PDF

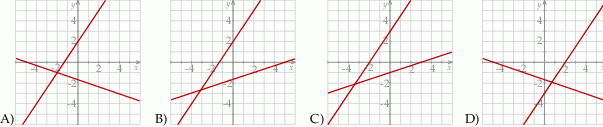
Rozwiązanie

Sposób I

Pierwsze równanie układu to prosta

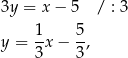
3y = x− 5 / : 3 1- 5- y = 3x − 3 ,

a drugie to prosta

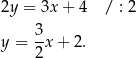
2y = 3x + 4 / : 2 3 y = --x+ 2. 2

Pierwsza prosta jest więc wykresem rosnącej funkcji liniowej, który przecina oś 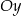Oy na poziomie 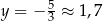5 y = − 3 ≈ 1,7 , a druga jest wykresem rosnącej funkcji liniowej, który przecina oś 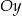Oy na poziomie 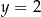y = 2 . Takie proste są narysowane na rysunku B.

Sposób II

Rozwiązujemy układ równań – odejmujemy od drugiego równania pierwsze pomnożone przez 3 (żeby skrócić x ).

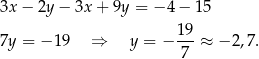
3x − 2y − 3x + 9y = − 4 − 15 1 9 7y = −1 9 ⇒ y = − --- ≈ − 2,7. 7

Z pierwszego równania mamy więc 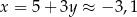x = 5 + 3y ≈ − 3 ,1 . Taka sytuacja jest przedstawiona na rysunku B.  
Odpowiedź: B

Wersja PDF