/Szkoła średnia/Zadania maturalne/Matura 2016
Lubelska próba przed maturą
z matematyki (dla klas pierwszych)
poziom podstawowy grupa I 2 czerwca 2015 Czas pracy: 170 minut
Zadania zamknięte
Wartość wyrażenia 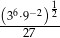 jest równa
jest równa
A) 3 B) 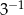 C)
C) 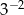 D)
D) 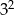
Odległość z Zamościa do Raciborza jest równa 468 km, natomiast po zaokrągleniu do pełnych setek 500 km. Błąd względny tego przybliżenia jest równy
A) 32 km B) 68 km C) 0,32% D) około 6,8%
Liczbą przeciwną do liczby 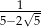 jest liczba:
jest liczba:
A) 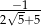 B)
B) 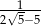 C)
C) 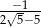 D)
D) 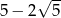
Jeśli, 120% pewnej liczby jest równe 480, to 75% tej liczby jest równe
A) 250 B) 300 C) 350 D) 400
Cięciwa dzieli okrąg na dwa łuki w stosunku 5:7. Miara kąta wpisanego opartego na krótszym łuku okręgu jest równa
A) 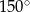 B)
B) 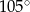 C)
C) 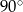 D)
D) 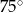
Wysokość trójkąta równobocznego o długości boku 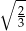 wynosi
wynosi
A) 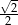 B)
B) 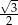 C)
C) 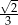 D)
D) 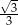
Jeden z kątów wewnętrznych trójkąta ma 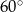 , a miary dwóch pozostałych kątów pozostają w stosunku jak 1:4. Miara kąta rozwartego tego trójkąta wynosi
, a miary dwóch pozostałych kątów pozostają w stosunku jak 1:4. Miara kąta rozwartego tego trójkąta wynosi
A) 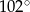 B)
B) 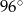 C)
C) 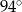 D)
D) 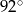
Liczba 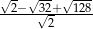 jest równa
jest równa
A) 7 B) 6 C) 5 D) 4
Rozwiązaniem nierówności 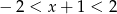 jest zbiór liczb
jest zbiór liczb
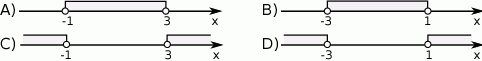
Pole rombu o długości boku 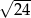 i kącie ostrym
i kącie ostrym 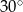 wynosi
wynosi
A) 24 B) 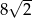 C) 11 D) 12
C) 11 D) 12
Dla jakiego argumentu funkcja 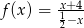 przyjmuje wartość 2?
przyjmuje wartość 2?
A) 1 B) 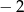 C)
C) 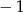 D) 2
D) 2
Pole trójkąta 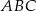 jest równe 17, a jego obwód 22. Jaki jest obwód trójkąta o polu 68, podobnego do trójkąta
jest równe 17, a jego obwód 22. Jaki jest obwód trójkąta o polu 68, podobnego do trójkąta 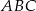 ?
?
A) 34 B) 44 C) 51 D) 88
Pole powierzchni całkowitej czworościanu foremnego o krawędzi równej 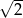 wynosi
wynosi
A) 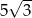 B)
B) 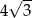 C)
C) 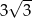 D)
D) 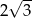
Jeżeli punkty 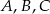 leżące na okręgu o środku
leżące na okręgu o środku 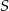 są wierzchołkami trójkąta równobocznego, to miara kąta środkowego
są wierzchołkami trójkąta równobocznego, to miara kąta środkowego 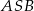 jest równa
jest równa
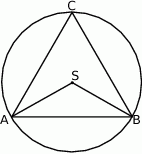
A) 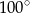 B)
B) 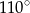 C)
C) 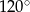 D)
D) 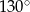
Wyrażenie 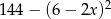 jest równe
jest równe
A) 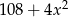 B)
B) 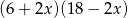 C)
C) 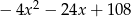 D)
D) 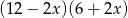
Dane są dwa okręgi o promieniach 27 i 11. Okręgi te są styczne wewnętrznie, gdy odległość między ich środkami jest równa
A) 38 B) 27 C) 16 D) 11
Ile liczb naturalnych dodatnich należy do zbioru rozwiązań układu nierówności
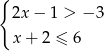
A) 4 B) 3 C) 2 D) 1
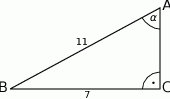
W trójkącie prostokątnym (patrz rysunek poniżej) tangens kąta ostrego  jest równy
jest równy
A) 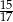 B)
B) 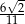 C)
C) 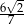 D)
D) 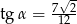
Jeśli wiadomo, że 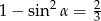 jest kątem ostrym, to prawdą jest, że
jest kątem ostrym, to prawdą jest, że
A) 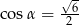 B)
B) 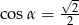 C)
C) 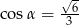 D)
D) 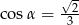
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Odległość dwóch liczb na osi liczbowej jest równa 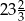 . Jeżeli mniejsza z tych liczb jest równa
. Jeżeli mniejsza z tych liczb jest równa 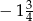 , to większa z tych liczb jest równa
, to większa z tych liczb jest równa
A) 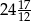 B)
B) 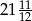 C)
C) 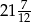 D)
D) 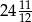
Ile wynosi tangens kąta  zaznaczonego na rysunku poniżej?
zaznaczonego na rysunku poniżej?
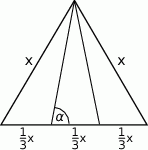
A) 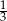 B)
B) 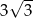 C)
C) 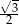 D)
D) 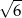
Dziedziną funkcji 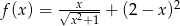 jest
jest
A) 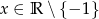 B)
B) 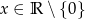 C)
C) 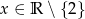 D)
D) 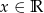
Liczba 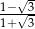 jest równa
jest równa
A) 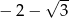 B)
B) 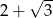 C)
C) 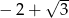 D)
D) 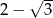
Zadania otwarte
Rozwiąż równanie 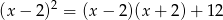 .
.
Cięciwa okręgu tworzy kąt 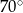 z promieniem przechodzącym przez jej koniec. Oblicz obydwa kąty środkowe wyznaczone przez tę cięciwę.
z promieniem przechodzącym przez jej koniec. Oblicz obydwa kąty środkowe wyznaczone przez tę cięciwę.
Uzasadnij, że równość 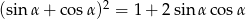 jest tożsamością trygonometryczną.
jest tożsamością trygonometryczną.
Liczby 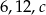 są długościami boków trójkąta równoramiennego. Oblicz długość boku
są długościami boków trójkąta równoramiennego. Oblicz długość boku  .
.
Uzasadnij, że suma dwóch liczb dwucyfrowych takich, że cyfra dziesiątek i cyfra jedności pierwszej z nich jest odpowiednio cyfrą jedności i cyfrą dziesiątek drugiej jest podzielna przez 11.
Stosunek pola trójkąta prostokątnego do pola kwadratu, zbudowanego na przeciwprostokątnej tego trójkąta jest równy 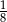 . Oblicz sumę tangensów kątów ostrych tego trójkąta.
. Oblicz sumę tangensów kątów ostrych tego trójkąta.
Janek jest o 6 lat młodszy od Michała. Za 30 lat będą mieli razem 104 lata. Ile lat ma każdy z nich obecnie?
Obwód prostokąta wynosi 60 cm. Jeśli krótszy bok tego prostokąta zwiększymy o 3 cm, a dłuższy skrócimy o 3 cm, to otrzymamy kwadrat. Wyznacz kąt pomiędzy przekątną, a dłuższym bokiem prostokąta. Wynik podaj z dokładnością do 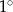 .
.
Z wykresu funkcji 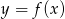 przedstawionego na rysunku odczytaj:
przedstawionego na rysunku odczytaj:
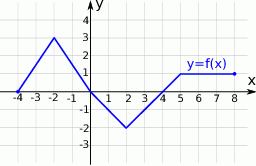
- dziedzinę i zbiór wartości funkcji;
- miejsca zerowe funkcji;
- maksymalne przedziały, w których funkcja jest rosnąca;
- dla jakich argumentów funkcja przyjmuje wartości większe od zera;
- zbiór rozwiązań nierówności
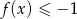 .
.

