/Gimnazjum/Egzamin gimnazjalny/Egzamin 2016
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 19 marca 2016 Czas pracy: 90 minut
Informacja do zadań 1 i 2
Promocja w zakładzie fryzjerskim jest związana z wiekiem klienta i polega na tym, że klient otrzymuje tyle procent zniżki, ile ma lat.
Ile za usługę fryzjerską zapłaci pani Leokadia, jeżeli koszt tej usługi bez promocji wynosi 160 zł, a Pani Leokadia ma 55 lat? Wybierz odpowiedź spośród podanych.
A) 72 zł B) 88 zł C) 105 zł D) 115 zł
Usługa fryzjerska bez promocji kosztuje 85 zł, a klient zgodnie z obowiązującą promocją musi za nią zapłacić 51 zł. Ile lat ma ten klient? Wybierz odpowiedź spośród podanych.
A) 60 B) 40 C) 45 D) 55
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Na osi liczbowej liczba 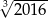 znajduje się między
znajduje się między
A) 40 i 50 B) 11 i 12 C) 12 i 13 D) 30 i 40
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Liczbą mniejszą od 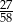 jest
jest
A) 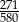 B)
B) 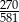 C)
C) 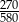 D)
D) 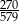
Poniżej podano kilka kolejnych potęg liczby 8.
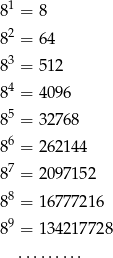
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Cyfrą jedności liczby 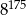 jest
jest
A) 4 B) 2 C) 8 D) 6
W zawodach sportowych każdy zawodnik miał pokonać trasę składającą się z trzech części. Pierwszą część trasy zawodnik przejechał na rowerze, drugą część – prowadzącą przez jezioro – przepłynął, a trzecią – przebiegł. Na rysunku przedstawiono schemat tej trasy.
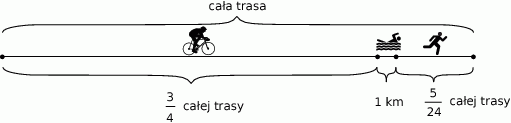
Na podstawie informacji wybierz zdanie prawdziwe.
A) Cała trasa miała długość 48 km.
B) Zawodnik przebiegł 10 km.
C) Odległość, którą zawodnik przebiegł, była o 4 km większa od odległości, którą przepłynął.
D) Odległość, którą zawodnik przejechał na rowerze, była 4 razy większa od odległości, którą przebiegł.
W klasie IIIa stosunek liczby chłopców do dziewcząt jest równy 3:2, a w klasie IIIb jest dwa razy więcej dziewcząt niż chłopców. Łącznie w obu tych klasach jest 24 chłopców i 28 dziewcząt. Na podstawie podanych informacji zapisano poniższy układ równań.
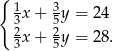
Co oznacza  w tym układzie równań? Wybierz właściwą odpowiedź spośród podanych.
w tym układzie równań? Wybierz właściwą odpowiedź spośród podanych.
A) Liczbę chłopców w klasie IIIa.
B) Liczbę chłopców w klasie IIIb.
C) Liczbę uczniów klasy IIIa.
D) Liczbę uczniów klasy IIIb.
Prędkość średnia piechura na trasie 9 km wyniosła 6 km/h, a prędkość średnia rowerzysty na tej samej trasie była równa 18 km/h. O ile minut więcej zajęło pokonanie tej trasy piechurowi niż rowerzyście? Wybierz odpowiedź spośród podanych.
A) 30 minut B) 60 minut C) 90 minut D) 120 minut
Sześcian o krawędzi długości 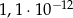 ma objętość równą
ma objętość równą
A) 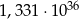 B)
B) 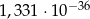 C)
C) 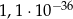 D)
D) 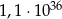
W konkursie przyznano nagrody pieniężne. Zdobywca trzeciego miejsca otrzymał 2500 zł. Nagroda za zdobycie drugiego miejsca była o 20% większa niż nagroda za zajęcie trzeciego miejsca. Nagroda za zdobycie pierwszego miejsca była o 40% większa niż nagroda za zajęcie drugiego miejsca.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Uczestnik konkursu, który zdobył pierwsze miejsce, otrzymał 4000 zł. | P | F |
| Nagroda za zdobycie pierwszego miejsca była o 68% większa od nagrody za zajęcie trzeciego miejsca. | P | F |
Ania z patyczków jednakowej długości buduje różne trójkąty

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Ania z 86 takich patyczków może zbudować trójkąt równoboczny | P | F |
| Ania z 48 takich patyczków może zbudować trójkąt prostokątny. | P | F |
Sześć różnych liczb naturalnych zapisano w kolejności od najmniejszej do największej:
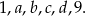
Mediana liczb: 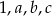 jest dwa razy mniejsza od mediany liczb
jest dwa razy mniejsza od mediany liczb 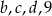 , a średnia arytmetyczna liczb
, a średnia arytmetyczna liczb 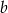 i
i  jest liczbą naturalną.
jest liczbą naturalną.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Mediana liczb  jest równa
jest równa
A) 5 B) 4 C) 6 D) 3
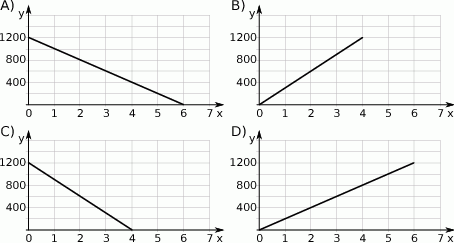
Wzór 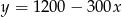 opisuje zależność objętości
opisuje zależność objętości 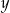 (w litrach) wody w zbiorniku od czasu
(w litrach) wody w zbiorniku od czasu  (w minutach) upływającego podczas opróżniania tego zbiornika. Który wykres przedstawia tę zależność? Wybierz właściwą odpowiedź spośród podanych.
(w minutach) upływającego podczas opróżniania tego zbiornika. Który wykres przedstawia tę zależność? Wybierz właściwą odpowiedź spośród podanych.
W prostokątnym układzie współrzędnych przedstawiono wykres funkcji.
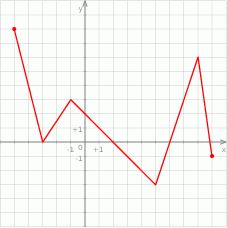
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Funkcja  dla argumentów ujemnych przyjmuje wartości dodatnie. dla argumentów ujemnych przyjmuje wartości dodatnie. | P | F |
Funkcja  pewną wartość przyjmuje dla 4 argumentów. pewną wartość przyjmuje dla 4 argumentów. | P | F |
Na rysunku przedstawiono okrąg wpisany w trójkąt.
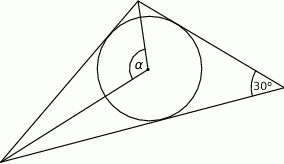
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Miara kąta  jest równa
jest równa
A) 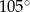 B)
B) 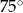 C)
C) 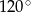 D)
D) 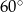
Rzucamy jeden raz sześcienną kostką do gry. Oznaczmy przez 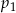 prawdopodobieństwo wyrzucenia liczby pierwszej, a przez
prawdopodobieństwo wyrzucenia liczby pierwszej, a przez 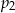 – prawdopodobieństwo wyrzucenia liczby złożonej.
– prawdopodobieństwo wyrzucenia liczby złożonej.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 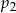 jest mniejsza od liczby jest mniejsza od liczby 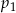 . . | P | F |
Liczby 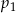 i i 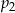 są mniejsze od są mniejsze od 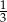 . . | P | F |
Szklane naczynie w kształcie stożka o promieniu podstawy 6 cm i wysokości 9 cm napełniono wodą do połowy wysokości (zobacz rysunek) i szczelnie zamknięto.
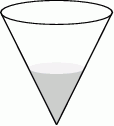
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Objętość wlanej wody stanowi  objętości naczynia. objętości naczynia. | P | F |
| Jeżeli naczynie odwrócimy i postawimy na podstawie stożka, to naczynie będzie wypełnione wodą do połowy wysokości. | P | F |
Jacek wyciął z kartki papieru dwa jednakowe trójkąty prostokątne o bokach długości 18 cm, 24 cm i 30 cm. Pierwszy z nich zagiął wzdłuż symetralnej dłuższej przyprostokątnej, a drugi – wzdłuż symetralnej krótszej przyprostokątnej. W ten sposób otrzymał czworokąty pokazane na rysunkach.
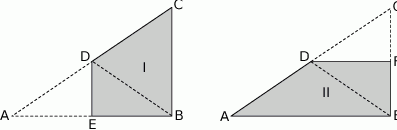
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Pole czworokąta I jest równe polu czworokąta II. | P | F |
| Obwód czworokąta I jest mniejszy od obwodu czworokąta II. | P | F |
Rozcinając powierzchnię boczną walca o promieniu  otrzymujemy kwadrat. Objętość tego walca wyraża się wzorem
otrzymujemy kwadrat. Objętość tego walca wyraża się wzorem
A) 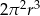 B)
B) 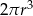 C)
C) 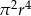 D)
D) 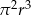
W układzie współrzędnych zaznaczono cztery kolejne wierzchołki sześciokąta  , który posiada środek symetrii.
, który posiada środek symetrii.
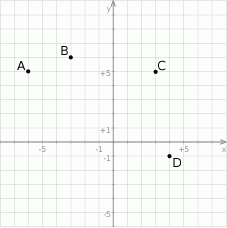
Który z podanych punktów jest jednym z wierzchołków tego sześciokąta?
A) 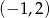 B)
B) 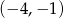 C)
C) 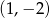 D)
D) 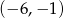
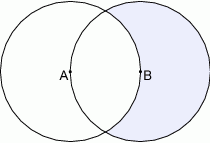
Na rysunku przedstawiono dwa koła o promieniu 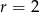 takie, że środek każdego z kół leży na brzegu drugiego koła. Oblicz pole powierzchni zacieniowanej części tej figury.
takie, że środek każdego z kół leży na brzegu drugiego koła. Oblicz pole powierzchni zacieniowanej części tej figury.
Olaf, Kacper i Łukasz kupowali słodycze. Olaf za 10 cukierków czekoladowych i 3 lizaki zapłacił 21 zł. Kacper kupił 6 cukierków czekoladowych i 6 lizaków i również zapłacił 21 zł. Czy Łukaszowi wystarczy 21 złotych na zakup 8 cukierków czekoladowych i 4 lizaków? Zapisz obliczenia i odpowiedź.
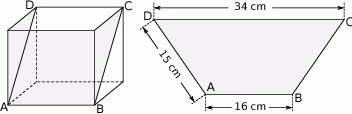
Powierzchnię boczną pudełka w kształcie graniastosłupa czworokątnego rozcięto wzdłuż przekątnych dwóch przeciwległych ścian bocznych i otrzymano dwa przystające trapezy. Podstawy otrzymanych trapezów mają długości 16 cm i 34 cm, a ich ramiona mają długość 15 cm. Oblicz objętość tego pudełka. Zapisz obliczenia.