/Gimnazjum/Egzamin gimnazjalny/Egzamin 2016
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 16 kwietnia 2016 Czas pracy: 90 minut
Informacja do zadań 1 i 2
Każda z dwóch wind towarowych obsługujących nowo budowany wieżowiec porusza się z prędkością 1,2 km/h. Na schemacie zaznaczono niektóre długości trasy pokonywanej przez windy.
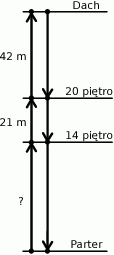
Jak długo trwa przejazd windy między dachem, a 14 piętrem? Wybierz właściwą odpowiedź spośród podanych.
A) 3 minuty B) 3 minuty i 9 sekund C) 6 minut i 18 sekund D) 4 minuty
Winda zaczyna zjeżdżać z dachu o 1 minutę i 24 sekundy później niż winda wyjeżdżająca z parteru. Obie windy w tym samym momencie dojeżdżają do 20 piętra. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość trasy windy pomiędzy parterem, a 14 piętrem jest równa
A) 49 metrów B) 42 metry C) 36 metrów D) 52 metry
Wartość wyrażenia 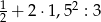 jest równa
jest równa
A) 2 B) 1,875 C)  D)
D) 
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe. Jeżeli przyjmiemy, że 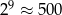 i
i 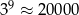 , to za przybliżenie liczby
, to za przybliżenie liczby 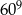 możemy przyjąć
możemy przyjąć
A) 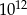 B)
B) 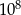 C)
C) 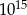 D)
D) 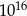
Dane jest przybliżenie 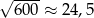 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
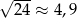 | P | F |
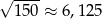 | P | F |
W dodatniej liczbie trzycyfrowej cyfra dziesiątek jest równa 7, a cyfra setek jest o 6 większa od cyfry jedności. Ile jest liczb spełniających te warunki?
Wybierz właściwą odpowiedź spośród podanych.
A) Jedna. B) Dwie. C) Trzy. D) Cztery.
Pan Kazimierz po 10% podwyżce zarabia 2695 zł miesięcznie.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Przed podwyżką pan Kazimierz zarabiał
A) 2500 zł. B) 2350 zł. C) 2400 zł. D) 2450 zł.
Na wykresie przedstawiono, jak zmienia się masa beczki z benzyną w zależności od objętości wlanej do niej benzyny.
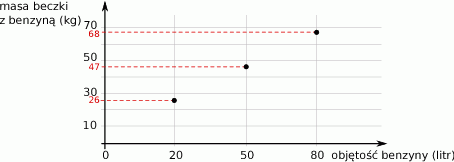
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Beczka, do której nalano 100 litrów benzyny waży 82 kg. | P | F |
| Beczka waży 15 kg. | P | F |
Ania jest 4 razy starsza od Pawła. Za 8 lat Ania i Paweł będą mieli w sumie 38 lat.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Jeżeli przez  oznaczymy wiek Pawła, a przez
oznaczymy wiek Pawła, a przez 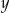 wiek Ani, to powyższą sytuację opisuje układ równań
wiek Ani, to powyższą sytuację opisuje układ równań
A) 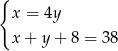 B)
B) 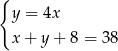 C)
C) 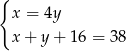 D)
D) 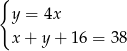
Doświadczenie losowe polega na dwukrotnym rzucie monetą. Jeśli wypadnie orzeł, zapisujemy 6, a jeśli reszka – zapisujemy 4. Wynikiem doświadczenia jest zapisana liczba dwucyfrowa. Jakie jest prawdopodobieństwo, że zapisana liczba jest podzielna przez 3? Wybierz właściwą odpowiedź spośród podanych.
A) 0 B) 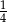 C)
C) 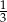 D)
D) 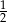
Na most długości 200 m wjechała ciężarówka o długości 20 m. Ciężarówka porusza się z prędkością 36 km/h. Ile czasu upłynie od momentu wjazdu kabiny ciężarówki na most do momentu całkowitego zjechania ciężarówki z mostu?
Wybierz odpowiedź spośród podanych.
A) 20 sekund B) 22 sekundy C) 200 sekund D) 24 sekundy
Dwie spośród liczb 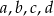 są dodatnie, a dwie ujemne.
są dodatnie, a dwie ujemne.
Ile najwięcej liczb ujemnych może być pośród liczb 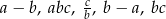 ? Wybierz właściwą odpowiedź spośród podanych.
? Wybierz właściwą odpowiedź spośród podanych.
A) Dwie. B) Trzy. C) Cztery. D) Pięć.
Obrazem okręgu 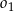 w symetrii względem punktu
w symetrii względem punktu 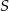 jest okrąg
jest okrąg 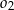 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Jeżeli okręgi 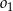 i i 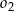 mają dwa punkty wspólne, to mają dwa punkty wspólne, to 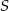 leży na zewnątrz koła ograniczonego okręgiem leży na zewnątrz koła ograniczonego okręgiem 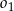 . . | P | F |
Jeżeli okręgi 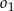 i i 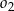 mają jeden punkt wspólny, to mają jeden punkt wspólny, to 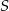 jest punktem okręgu jest punktem okręgu 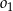 . . | P | F |
Jeżeli 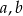 i
i  są długościami boków trójkąta oraz
są długościami boków trójkąta oraz  jest jego najdłuższym bokiem, to ten trójkąt jest:
jest jego najdłuższym bokiem, to ten trójkąt jest:
– prostokątny, gdy 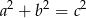
– rozwartokątny, gdy 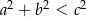
– ostrokątny, gdy 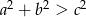 .
.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Z odcinków o długościach: 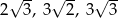
A) nie można zbudować trójkąta.
B) można zbudować trójkąt prostokątny.
C) można zbudować trójkąt rozwartokątny.
D) można zbudować trójkąt ostrokątny.
Który z zaznaczonych kątów jest kątem środkowym?
Zaznacz poprawną odpowiedź.
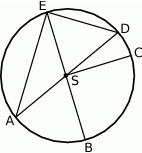
A) 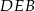 B)
B) 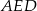 C)
C) 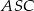 D)
D) 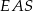
W poniższej tabeli zebrano zarobki wszystkich pracowników pewnej firmy handlowej.
| Imię pracownika | Zarobki |
| Kamila, Krzysztof, Stefan | 2800 zł |
| Zofia, Łukasz | 3000 zł |
| Ela, Marta | 3200 zł |
| Henryk | 3600 zł. |
Jaka jest średnia zarobków pracowników tej firmy? Wybierz odpowiedź spośród podanych.
A) 3050 zł B) 3150 zł C) 3200 zł D) 3250 zł
Na rysunku przedstawiono sześciokąt foremny 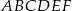 o boku równym 1 cm.
o boku równym 1 cm.
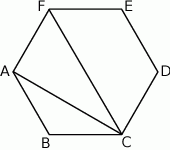
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Przekątna 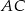 ma długość ma długość 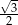 . . | P | F |
Przekątna 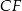 ma długość ma długość 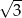 . . | P | F |
Rysunki przedstawiają bryłę, której wszystkie cztery ściany są trójkątami równobocznymi.

Które wielokąty – I, II, III – przedstawiają siatki bryły takiej, jaką pokazano na powyższych rysunkach? Wybierz właściwą odpowiedź spośród podanych.
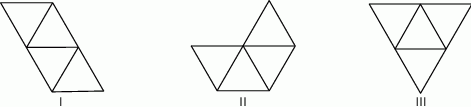
A) I, II i III B) tylko I i III C) tylko II i III D) tylko I i II
Końce odcinka 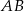 mają współrzędne
mają współrzędne 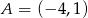 i
i 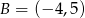 . Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
. Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Na symetralnej odcinka 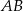 leży punkt o współrzędnych
leży punkt o współrzędnych
A) 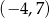 B)
B) 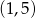 C)
C) 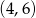 D)
D) 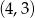
Na rysunku przedstawiono ostrosłup prawidłowy trójkątny oraz graniastosłup prawidłowy trójkątny. Bryły mają jednakowe podstawy i równe wysokości, a iloczyn objętości tych brył jest równy 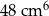 .
.
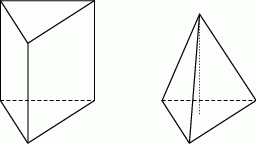
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Objętość ostrosłupa jest równa 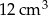 . . | P | F |
| Objętość graniastosłupa jest trzy razy większa od objętości ostrosłupa. | P | F |
Suma cyfr liczby trzycyfrowej podzielnej przez 5 jest równa 15. Jeśli zapiszemy cyfry tej liczby w odwrotnej kolejności, to otrzymamy liczbę o 198 większą od początkowej. Wyznacz liczbę początkową.
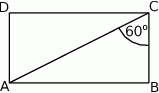
Przekątna prostokąta 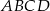 nachylona jest do jednego z jego boków pod kątem
nachylona jest do jednego z jego boków pod kątem 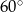 . Uzasadnij, że pole prostokąta
. Uzasadnij, że pole prostokąta  jest równe polu trójkąta równobocznego o boku równym przekątnej tego prostokąta.
jest równe polu trójkąta równobocznego o boku równym przekątnej tego prostokąta.
Przekrój osiowy stożka jest trójkątem równobocznym o polu 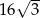 . Oblicz objętość i pole powierzchni całkowitej tego stożka.
. Oblicz objętość i pole powierzchni całkowitej tego stożka.

