/Gimnazjum/Egzamin gimnazjalny/Egzamin 2016
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 9 kwietnia 2016 Czas pracy: 90 minut
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Różnica między największą i najmniejszą spośród liczb:
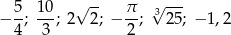
jest równa
A) 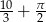 B)
B) 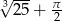 C)
C) 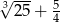 D)
D) 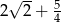
Dokończ zdanie. Zaznacz dobrą odpowiedź.
Liczbą podzielną przez 36 jest
A) 345222 B) 986472 C) 322144 D) 631422
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Na osi liczbowej liczba równa wartości wyrażenia arytmetycznego 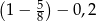 znajduje się między
znajduje się między
A) 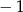 i
i 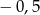 B)
B) 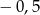 i 0 C) 0 i 0,5 D) 0,5 i 1
i 0 C) 0 i 0,5 D) 0,5 i 1
Ile jest liczb całkowitych, dla których wyrażenie 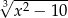 nie może być obliczone w zbiorze liczb rzeczywistych?
nie może być obliczone w zbiorze liczb rzeczywistych?
A) 0 B) 3 C) 6 D) 7
Na tablicy zaczęto wypisywać kolejne liczby naturalne, które przy dzieleniu przez 4 dają resztę 3.
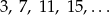
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Cyfrą jedności dwusetnej z napisanych liczb jest
A) 3 B) 7 C) 5 D) 9
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe. Powierzchnia 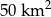 jest równa
jest równa
A) 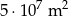 B)
B) 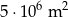 C)
C) 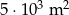 D)
D) 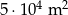
Zmieszano dwa gatunki kawy, droższą i tańszą, w stosunku 1:4. Cena jednego kilograma tej mieszanki kaw wynosi 110 zł. Gdyby te kawy zmieszano w stosunku 2:3, to cena za 1 kg tej mieszanki wynosiłaby 120 zł. Na podstawie podanych informacji zapisano poniższy układ równań.
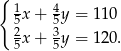
Co oznacza 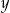 w tym układzie równań? Wybierz właściwą odpowiedź spośród podanych.
w tym układzie równań? Wybierz właściwą odpowiedź spośród podanych.
A) Cenę 1 kg kawy droższej.
B) Cenę 1 kg kawy tańszej.
C) Cenę 5 kg kawy droższej.
D) Cenę 5 kg kawy tańszej.
Na wykresie przedstawiono wysokość zarobków 6 pracowników pewnego przedsiębiorstwa.
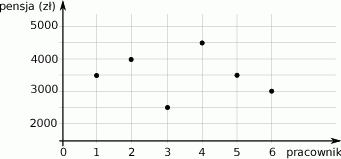
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli każdy z pierwszych 3 pracowników otrzyma 10% podwyżkę, to łącznie będą zarabiać więcej niż w sumie zarabiają pracownicy nr 4, 5 i 6. | P | F |
| Zarobki pracownika nr 5 są o 36% wyższe od zarobków pracownika nr 3. | P | F |
Informacja do zadań 9 i 10
Jedną z jednostek używanych do mierzenia kątów są grady. Tworząc te jednostki dzielimy kąt pełny na 400 gradów.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe. Miara w stopniach kąta o mierze 220 gradów jest równa
A) 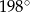 B)
B) 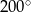 C)
C) 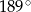 D)
D) 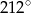
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe. Kąt prosty wyrażony w gradach to
A) 150 gradów B) 200 gradów C) 100 gradów D) 50 gradów
Pięć różnych liczb naturalnych zapisano w kolejności od najmniejszej do największej: 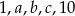 . Mediana liczb:
. Mediana liczb: 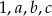 jest równa 3, a mediana liczb:
jest równa 3, a mediana liczb: 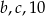 jest równa 8.
jest równa 8.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba 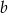 jest równa
jest równa
A) 4 B) 5 C) 6 D) 7
Dwa kąty trójkąta 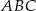 mają miary
mają miary 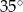 i
i 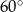 .
.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Trójkąt podobny do trójkąta 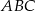 może mieć kąty o miarach
może mieć kąty o miarach
A) 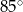 i
i 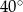 B)
B) 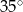 i
i 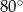 C)
C) 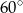 i
i 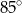 D)
D) 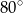 i
i 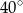
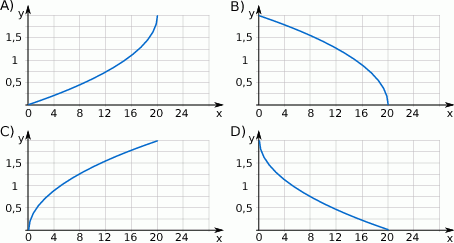
Piłkę tenisową puszczono swobodnie z pewnej wysokości. Wzór 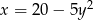 opisuje zależność wysokości
opisuje zależność wysokości  (w metrach) na jakiej znajduje się piłka od czasu
(w metrach) na jakiej znajduje się piłka od czasu 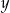 (w sekundach), który upłynął od momentu puszczenia piłki. Który wykres przedstawia tę zależność? Wybierz właściwą odpowiedź spośród podanych.
(w sekundach), który upłynął od momentu puszczenia piłki. Który wykres przedstawia tę zależność? Wybierz właściwą odpowiedź spośród podanych.
Łukasz wyciął z kartki papieru trójkąt równoramienny 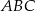 , a następnie zagiął w nim dwa narożniki tak, że wierzchołki
, a następnie zagiął w nim dwa narożniki tak, że wierzchołki 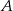 i
i 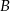 trójkąta znalazły się w środku
trójkąta znalazły się w środku 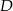 jego podstawy. Powstał w ten sposób pięciokąt
jego podstawy. Powstał w ten sposób pięciokąt 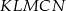 .
.
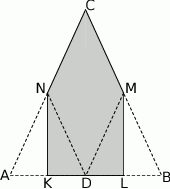
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole pięciokąta 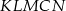 stanowi 75% pola trójkąta stanowi 75% pola trójkąta 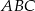 . . | P | F |
Obwód pięciokąta 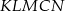 jest taki sam jak obwód trójkąta jest taki sam jak obwód trójkąta 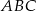 . . | P | F |
Proste 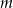 i
i  są styczne do okręgu i przecinają się pod kątem
są styczne do okręgu i przecinają się pod kątem 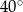 .
.
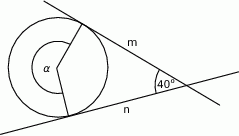
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Miara kąta  jest równa
jest równa
A) 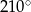 B)
B) 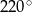 C)
C) 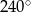 D)
D) 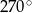
Pole działki budowlanej jest równe 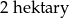 . Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
A) 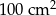 B)
B) 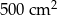 C)
C) 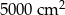 D)
D) 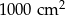
W układzie współrzędnych zaznaczono wierzchołki sześciokąta 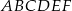 :
: 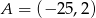 ,
, 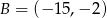 ,
, 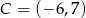 ,
, 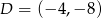 ,
, 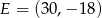 ,
, 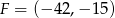 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trzy wierzchołki sześciokąta 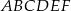 znajdują się w drugiej ćwiartce układu współrzędnych. znajdują się w drugiej ćwiartce układu współrzędnych. | P | F |
Dwa wierzchołki sześciokąta 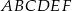 znajdują się w trzeciej ćwiartce układu współrzędnych. znajdują się w trzeciej ćwiartce układu współrzędnych. | P | F |
Do pudełka włożono 48 kul w różnych kolorach. Prawdopodobieństwo wylosowania kuli czerwonej jest równe 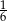 , a prawdopodobieństwo wylosowania kuli żółtej jest równe
, a prawdopodobieństwo wylosowania kuli żółtej jest równe 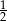 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W pudełku jest trzy więcej kul czerwonych niż żółtych. | P | F |
| W pudełku może być 16 kul zielonych. | P | F |
Szklane naczynie w kształcie prostopadłościanu o wymiarach 9 cm, 12 cm i 21 cm napełniono częściowo wodą i szczelnie zamknięto. Następnie naczynie postawiono na jego ścianie o największej powierzchni i wtedy woda sięgała do wysokości 6 cm.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Kiedy naczynie postawiono na ścianie o najmniejszej powierzchni, to woda sięgała do wysokości
A) 8 cm B) 10 cm C) 12 cm D) 14 cm
Promień kuli jest równy 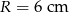 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Objętość tej kuli jest równa 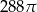 . . | P | F |
Pole powierzchni tej kuli jest równe 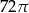 . . | P | F |
Miejscowości 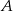 i
i 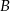 są połączone linią kolejową. Pociąg przebywa trasę z
są połączone linią kolejową. Pociąg przebywa trasę z 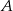 do
do 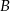 ze średnią prędkością 80 km/h. W drodze powrotnej średnia prędkość pociągu jest większa o 20 km/h i dzięki temu pociąg pokonuje trasę od
ze średnią prędkością 80 km/h. W drodze powrotnej średnia prędkość pociągu jest większa o 20 km/h i dzięki temu pociąg pokonuje trasę od 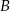 do
do 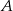 w czasie o godzinę krótszym. Jaka jest długość linii kolejowej między miejscowościami
w czasie o godzinę krótszym. Jaka jest długość linii kolejowej między miejscowościami 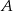 i
i 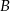 ?
?
Przez punkty 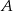 i
i 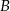 okręgu poprowadzono styczne, które przecięły się w punkcie
okręgu poprowadzono styczne, które przecięły się w punkcie 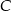 .
.
Wykaż, że jeżeli 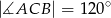 , to cięciwa
, to cięciwa 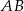 ma długość równą długości promienia okręgu.
ma długość równą długości promienia okręgu.
Po rozklejeniu ściany bocznej pudełka mającego kształt walca otrzymano równoległobok. Jeden z boków tej figury ma długość 33 cm, a jej pole jest równe 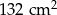 . Oblicz objętość tego pudełka. Przyjmij przybliżenie
. Oblicz objętość tego pudełka. Przyjmij przybliżenie 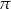 równe
równe 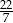 . Zapisz obliczenia.
. Zapisz obliczenia.


