/Szkoła średnia/Zadania maturalne/Matura 2016/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 23 kwietnia 2016 Czas pracy: 170 minut
Zadania zamknięte
Liczba 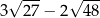 jest równa
jest równa
A) 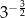 B)
B) 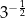 C)
C) 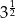 D)
D) 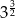
Cena długopisu po 2 podwyżkach o 20% i trzech obniżkach o 50% zmalała o 2,87 zł. Nowa cena długopisu jest równa
A) 1,26 zł B) 0,63 zł C) 3,50 zł D) 6,37 zł
Wartość wyrażenia 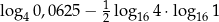 jest równa
jest równa
A) 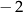 B)
B) 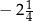 C)
C) 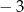 D) 0
D) 0
Równość 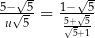 zachodzi dla
zachodzi dla
A) 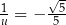 B)
B) 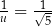 C)
C) 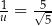 D)
D) 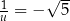
Iloczyn pierwszych 5 wyrazów ciągu geometrycznego danego wzorem 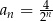 , gdzie
, gdzie 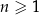 jest równy
jest równy
A)  B)
B) 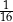 C)
C) 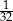 D)
D) 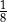
Równanie 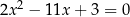
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dwa dodatnie rozwiązania rzeczywiste.
D) ma dwa ujemne rozwiązania rzeczywiste.
Jeżeli wykres funkcji 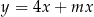 nie ma punktów wspólnych z prostą
nie ma punktów wspólnych z prostą 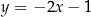 to
to
A) 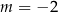 B)
B) 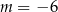 C)
C) 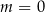 D)
D) 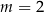
Na rysunku przedstawiono wykres funkcji 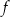 .
.

Zbiorem wartości funkcji 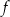 jest przedział
jest przedział
A) 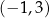 B)
B) 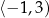 C)
C) 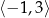 D)
D) 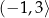
Iloczyn rozwiązań równania 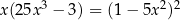 jest równy
jest równy
A) 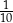 B)
B) 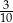 C)
C) 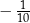 D)
D) 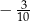
Prosta 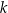 przecina oś
przecina oś 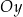 układu współrzędnych w punkcie
układu współrzędnych w punkcie 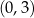 i jest prostopadła do prostej o równaniu
i jest prostopadła do prostej o równaniu 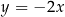 . Wówczas prosta
. Wówczas prosta 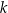 przecina oś
przecina oś 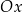 układu współrzędnych w punkcie
układu współrzędnych w punkcie
A) 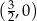 B)
B) 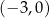 C)
C) 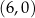 D)
D) 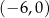
Wykres funkcji 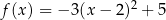 przesunięto o 3 jednostki w lewo i 2 jednostki w górę. W wyniku tej operacji otrzymano wykres funkcji
przesunięto o 3 jednostki w lewo i 2 jednostki w górę. W wyniku tej operacji otrzymano wykres funkcji
A) 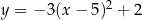 B)
B) 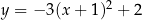
C) 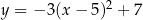 D)
D) 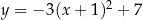
Ile liczb całkowitych  spełnia nierówność
spełnia nierówność 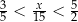 ?
?
A) 27 B) 28 C) 29 D) 30
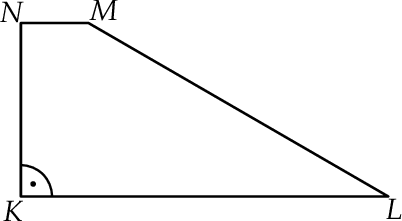
W trapezie 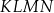 , w którym
, w którym 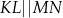 , kąt
, kąt 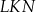 jest prosty (zobacz rysunek) oraz dane są:
jest prosty (zobacz rysunek) oraz dane są: 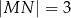 ,
, 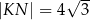 ,
, 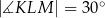 . Pole tego trapezu jest równe:
. Pole tego trapezu jest równe:
A) 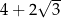 B)
B) 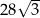 C)
C) 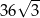 D)
D) 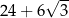
Suma dwudziestu początkowych wyrazów pewnego ciągu arytmetycznego jest 6 razy większa od sumy dziesięciu początkowych wyrazów tego ciągu. Wynika stąd, że suma drugiego i czwartego wyrazu tego ciągu jest równa
A) 0 B) 2 C) 8 D) 6
Ciąg liczbowy określony jest wzorem 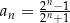 , dla
, dla 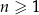 . Szósty wyraz tego ciągu jest równy
. Szósty wyraz tego ciągu jest równy
A) 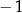 B)
B) 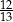 C)
C) 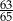 D) 1
D) 1
Punkty 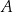 i
i 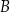 dzielą okrąg na dwa łuki, przy czym miary kątów wpisanych opartych na tych łukach różnią się o
dzielą okrąg na dwa łuki, przy czym miary kątów wpisanych opartych na tych łukach różnią się o 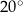 . Wynika stąd, że większy z tych katów ma miarę
. Wynika stąd, że większy z tych katów ma miarę
A) 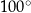 B)
B) 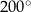 C)
C) 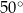 D)
D) 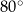
Sinus kąta ostrego  jest równy
jest równy 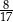 . Wówczas
. Wówczas
A) 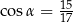 B)
B) 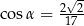 C)
C) 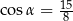 D)
D) 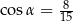
Boki trójkąta mają długości 30 i 8, a kąt między tymi bokami ma miarę 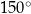 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 60 B) 120 C) 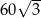 D)
D) 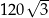
Ile jest wszystkich liczb czterocyfrowych, większych 3200, utworzonych wyłącznie z cyfr 1, 2, 3, przy założeniu, że cyfry mogą się powtarzać, ale nie wszystkie z tych cyfr muszą być wykorzystane?
A) 9 B) 6 C) 18 D) 27
Dane są punkty 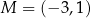 i
i 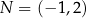 . Punkt
. Punkt 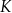 jest środkiem odcinka
jest środkiem odcinka 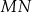 . Obrazem punktu
. Obrazem punktu 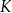 w symetrii względem początku układu współrzędnych jest punkt
w symetrii względem początku układu współrzędnych jest punkt
A) 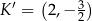 B)
B) 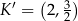 C)
C) 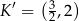 D)
D) 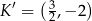
Suma liczby wierzchołków i liczby krawędzi graniastosłupa może być równa
A) 2017 B) 2016 C) 2015 D) 2014
Przekątna przekroju osiowego walca jest o 13 dłuższa od promienia podstawy tego walca, oraz o 2 dłuższa od jego wysokości. Pole podstawy tego walca jest równe
A) 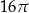 B)
B) 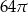 C)
C) 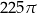 D)
D) 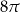
Średnia arytmetyczna zestawu danych: 7, 12, 8, 6,  ,
, 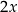 jest taka sama jak średnia arytmetyczna zestawu danych: 11, 8, 9, 3,
jest taka sama jak średnia arytmetyczna zestawu danych: 11, 8, 9, 3,  ,
,  ,
, 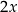 . Wynika stąd, że
. Wynika stąd, że
A) 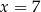 B)
B) 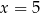 C)
C) 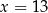 D)
D) 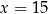
Zadania otwarte
Rozwiąż nierówność 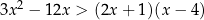 .
.
Wykaż, że dla wszystkich dodatnich liczb rzeczywistych 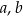 prawdziwa jest nierówność
prawdziwa jest nierówność 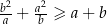 .
.
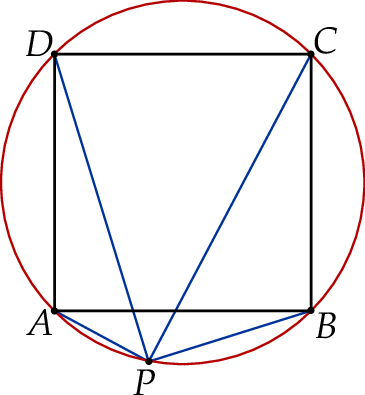
Punkt 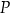 należy do okręgu opisanego na kwadracie
należy do okręgu opisanego na kwadracie 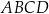 . Wykaż, że
. Wykaż, że 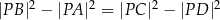 .
.
Niech 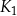 będzie kwadratem o boku długości
będzie kwadratem o boku długości  . Konstruujemy kolejno kwadraty
. Konstruujemy kolejno kwadraty 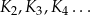 takie, że bok kolejnego kwadratu jest równy przekątnej poprzedniego kwadratu. Oblicz sumę pól kwadratów
takie, że bok kolejnego kwadratu jest równy przekątnej poprzedniego kwadratu. Oblicz sumę pól kwadratów 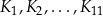 .
.
Ze zbioru liczb dwucyfrowych losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że iloczyn cyfr wylosowanej liczby jest dodatnią liczbą złożoną?
Dany jest prostokąt o bokach  i
i 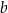 oraz prostokąt o bokach
oraz prostokąt o bokach  i
i 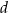 . Długość boku
. Długość boku  to 80% długości boku
to 80% długości boku  . Długość boku
. Długość boku 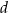 to 140% długości boku
to 140% długości boku 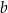 . Oblicz, ile procent pola prostokąta o bokach
. Oblicz, ile procent pola prostokąta o bokach  i
i 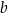 stanowi pole prostokąta o bokach
stanowi pole prostokąta o bokach  i
i 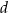 .
.
Wyznacz współrzędne punktu przecięcia się przekątnych czworokąta 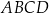 jeżeli
jeżeli 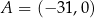 ,
, 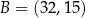 ,
, 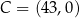 i
i 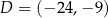 .
.
Na rysunku przedstawiono kwadrat 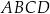 o polu 4.
o polu 4.
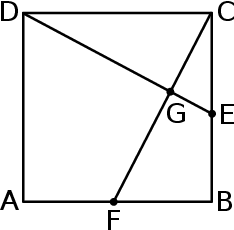
Punkty 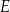 i
i 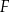 są środkami boków
są środkami boków 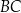 i
i 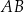 , a punkt
, a punkt 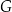 jest punktem wspólnym odcinków
jest punktem wspólnym odcinków 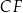 i
i 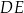 . Oblicz pole czworokąta
. Oblicz pole czworokąta 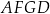
W nieskończonym ciągu arytmetycznym 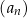 , określonym dla
, określonym dla 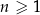 , suma dziewięciu początkowych wyrazów jest równa 171. Średnia arytmetyczna pierwszego, trzeciego i ósmego wyrazu tego ciągu, jest równa 15. Wyrazy
, suma dziewięciu początkowych wyrazów jest równa 171. Średnia arytmetyczna pierwszego, trzeciego i ósmego wyrazu tego ciągu, jest równa 15. Wyrazy 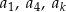 ciągu
ciągu 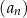 , w podanej kolejności, tworzą nowy ciąg – trzywyrazowy ciąg geometryczny
, w podanej kolejności, tworzą nowy ciąg – trzywyrazowy ciąg geometryczny 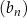 . Oblicz
. Oblicz 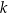 .
.
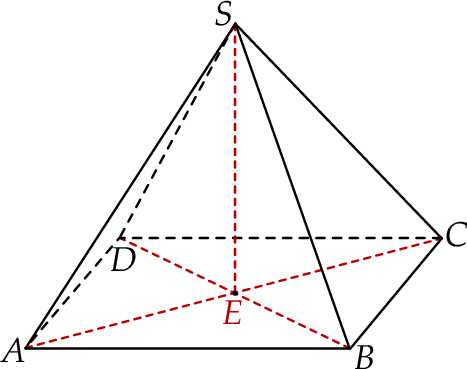
Podstawą ostrosłupa 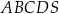 jest prostokąt, którego boki pozostają w stosunku 5:12, a pole jest równe 240 (zobacz rysunek). Punkt
jest prostokąt, którego boki pozostają w stosunku 5:12, a pole jest równe 240 (zobacz rysunek). Punkt 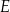 jest wyznaczony przez przecinające się przekątne podstawy, a odcinek
jest wyznaczony przez przecinające się przekątne podstawy, a odcinek 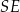 jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem
jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 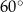 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.