/Szkoła średnia/Zadania maturalne/Matura 2016/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 23 kwietnia 2016 Czas pracy: 180 minut
Zadania zamknięte
Na rysunku przedstawiony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność 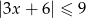 .
.
![]()
Stąd wynika, że
A) 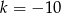 B)
B) 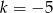 C)
C) 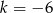 D)
D) 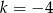
Liczba rzeczywistych pierwiastków równania 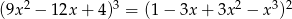 jest równa
jest równa
A) 4 B) 2 C) 1 D) 0
Wielomian 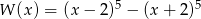 zapisano w postaci
zapisano w postaci 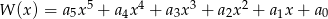 . Suma
. Suma 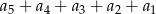 jest równa
jest równa
A) 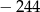 B)
B) 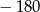 C)
C) 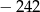 D)
D) 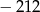
Dla dowolnego kąta  wartość wyrażenia
wartość wyrażenia 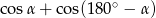 jest równa wartości wyrażenia
jest równa wartości wyrażenia
A) 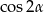 B)
B) 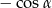 C)
C) 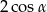 D) 0
D) 0
Punkt 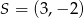 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 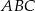 . Prosta zawierająca bok
. Prosta zawierająca bok 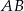 tego trójkąta ma równanie
tego trójkąta ma równanie 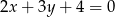 . Prosta zawierająca bok
. Prosta zawierająca bok 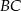 może mieć równanie
może mieć równanie
A) 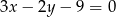 B)
B) 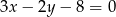 C)
C) 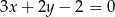 D)
D) 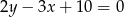
Zadania otwarte
Wyznacz najmniejszą liczbę całkowitą spełniającą nierówność 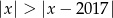 .
.
Oblicz 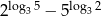 .
.
Oblicz granicę funkcji 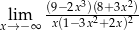 .
.
Średnia arytmetyczna  początkowych wyrazów ciągu
początkowych wyrazów ciągu 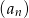 jest równa
jest równa 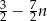 . Wyznacz wzór ogólny ciągu
. Wyznacz wzór ogólny ciągu 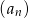 .
.
Okrąg 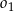 przechodzi przez wierzchołek
przechodzi przez wierzchołek 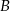 trójkąta
trójkąta 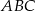 i przecina jego boki
i przecina jego boki 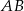 i
i 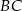 odpowiednio w punktach
odpowiednio w punktach 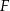 i
i 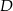 . Okrąg
. Okrąg 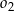 przechodzi przez wierzchołek
przechodzi przez wierzchołek 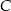 , przecina okrąg
, przecina okrąg 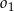 w punkcie
w punkcie 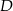 oraz w punkcie
oraz w punkcie 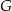 leżącym wewnątrz trójkąta
leżącym wewnątrz trójkąta 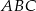 . Ponadto okrąg
. Ponadto okrąg 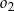 przecina bok
przecina bok 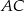 trójkąta w punkcie
trójkąta w punkcie 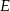 .
.
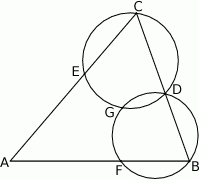
Udowodnij, że punkt 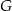 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 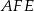 .
.
W fabryce obuwia pracuje pięć linii produkcyjnych produkujących ten sam model butów. W poniższej tabeli zawarto informacje o wydajności tych linii oraz o odsetku wadliwych par obuwia produkowanych przez każdą z nich.
| Linia produkcyjna | Wydajność | Odsetek wadliwych par |
| I | 60 par/godzinę | 2% |
| II | 50 par/godzinę | 3% |
| III | 40 par/godzinę | 1% |
| IV | 80 par/godzinę | 3% |
| V | 70 par/godzinę | 2% |
Wybieramy losowo jedną parę obuwia wyprodukowaną przez te linie produkcyjne. Jakie jest prawdopodobieństwo, że wybrana para nie okaże się wadliwa?
Wykaż, że istnieje liczba dodatnia  , dla której
, dla której 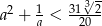 .
.
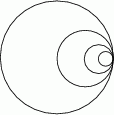
Dany jest okrąg 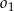 o promieniu
o promieniu  . Wewnątrz tego okręgu narysowano okrąg
. Wewnątrz tego okręgu narysowano okrąg 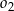 styczny wewnętrznie o średnicy
styczny wewnętrznie o średnicy  , wewnątrz okręgu
, wewnątrz okręgu 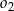 znów narysowano okrąg styczny wewnętrznie o średnicy
znów narysowano okrąg styczny wewnętrznie o średnicy 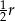 itd. Czynność tę powtórzono nieskończenie wiele razy. Wykaż, że suma długości okręgów
itd. Czynność tę powtórzono nieskończenie wiele razy. Wykaż, że suma długości okręgów 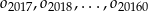 jest mniejsza od długości okręgu
jest mniejsza od długości okręgu 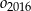 .
.
W trójkąt prostokątny 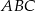 o przyprostokątnych długości
o przyprostokątnych długości 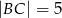 i
i 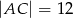 wpisano okrąg. Oblicz długość odcinka łączącego punkty wspólne okręgu wpisanego z bokami
wpisano okrąg. Oblicz długość odcinka łączącego punkty wspólne okręgu wpisanego z bokami 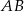 i
i 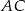 .
.
Do windy na parterze budynku wsiadło 6 osób, po czym każda z nich w sposób losowy wysiadła na jednym z trzech pięter budynku. Jakie jest prawdopodobieństwo, że na jednym z pięter wysiadły dokładnie 4 osoby?
Oblicz pole trójkąta ograniczonego osią 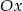 oraz stycznymi do wykresu funkcji
oraz stycznymi do wykresu funkcji 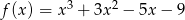 poprowadzonymi w punktach
poprowadzonymi w punktach 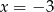 i
i 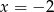 .
.
Funkcja 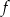 jest określona wzorem
jest określona wzorem 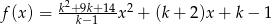 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz całkowite wartości parametru
. Wyznacz całkowite wartości parametru 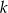 , dla których funkcja
, dla których funkcja 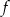 przyjmuje wartość największą i ma dwa różne miejsca zerowe o jednakowych znakach.
przyjmuje wartość największą i ma dwa różne miejsca zerowe o jednakowych znakach.
Romb o boku długości  obraca się dokoła jednej z przekątnych. Wyznacz pole tego spośród takich rombów, dla którego objętość otrzymanej bryły jest największa.
obraca się dokoła jednej z przekątnych. Wyznacz pole tego spośród takich rombów, dla którego objętość otrzymanej bryły jest największa.

