/Szkoła średnia/Zadania maturalne/Matura 2016/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 19 marca 2016 Czas pracy: 180 minut
Zadania zamknięte
Na rysunku przedstawiony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność 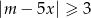 .
.
![]()
Stąd wynika, że
A) 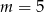 B)
B) 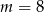 C)
C) 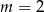 D)
D) 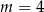
Dany jest wielomian 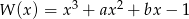 , gdzie
, gdzie  i
i 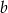 są liczbami całkowitymi. Zatem
są liczbami całkowitymi. Zatem
A) Jeżeli równanie 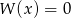 ma pierwiastek wymierny, to
ma pierwiastek wymierny, to 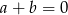 .
.
B) Jeżeli równanie 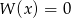 ma ujemny pierwiastek całkowity, to
ma ujemny pierwiastek całkowity, to 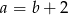 .
.
C) Równanie 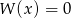 może nie mieć rozwiązań.
może nie mieć rozwiązań.
D) Równanie 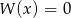 musi mieć co najmniej 2 różne pierwiastki.
musi mieć co najmniej 2 różne pierwiastki.
Pochodna funkcji 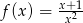 jest równa
jest równa
A) 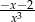 B)
B) 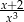 C)
C) 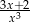 D)
D) 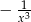
Wartość wyrażenia 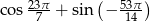 jest równa
jest równa
A) 0 B) 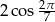 C)
C) 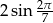 D)
D) 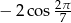
Wskaż równanie okręgu stycznego do prostej 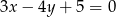 .
.
A) 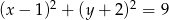
B) 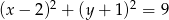
C) 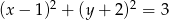
D) 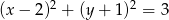
Zadania otwarte
Oblicz granicę jednostronną funkcji 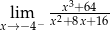 .
.
Punkt 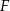 jest środkiem boku
jest środkiem boku 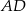 prostokąta
prostokąta 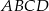 , w którym
, w którym 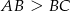 . Punkt
. Punkt 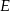 jest takim punktem boku
jest takim punktem boku  tego prostokąta, że prosta
tego prostokąta, że prosta 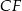 jest dwusieczną kąta
jest dwusieczną kąta 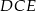 . Wykaż, że trójkąt
. Wykaż, że trójkąt 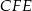 jest prostokątny.
jest prostokątny.
Udowodnij, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność
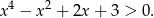
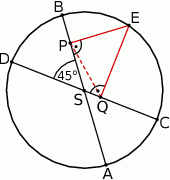
W okręgu o promieniu 6 średnice 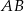 i
i 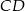 przecinają się pod kątem
przecinają się pod kątem 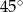 . Na okręgu tym wybrano punkt
. Na okręgu tym wybrano punkt 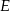 oraz skonstruowano jego rzuty
oraz skonstruowano jego rzuty 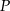 i
i 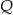 odpowiednio na średnice
odpowiednio na średnice 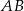 i
i  . Oblicz długość odcinka
. Oblicz długość odcinka  .
.
Funkcja  określona jest wzorem
określona jest wzorem 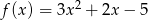 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 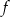 , które przechodzą przez punkt
, które przechodzą przez punkt 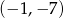 .
.
Rozwiąż nierówność 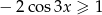 w przedziale
w przedziale 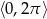 .
.
W trójkąt równoramienny 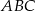 o podstawie długości
o podstawie długości 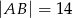 i polu 168 wpisano okrąg. Oblicz długość odcinka łączącego wierzchołek
i polu 168 wpisano okrąg. Oblicz długość odcinka łączącego wierzchołek 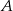 z punktem wspólnym okręgu i ramienia
z punktem wspólnym okręgu i ramienia 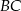 .
.
Odcinek 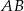 o długości 20 jest zawarty w prostej o równaniu
o długości 20 jest zawarty w prostej o równaniu 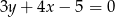 . Symetralna odcinka
. Symetralna odcinka 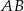 przecina oś
przecina oś 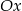 w punkcie
w punkcie 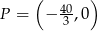 . Oblicz współrzędne końców odcinka
. Oblicz współrzędne końców odcinka 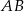 .
.
Oblicz prawdopodobieństwo warunkowe, że w czterokrotnym rzucie symetryczną sześcienną kostką do gry otrzymamy co najmniej jedną „czwórkę”, pod warunkiem że otrzymamy co najmniej jedną „piątkę”.
Funkcja kwadratowa 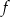 jest określona wzorem
jest określona wzorem 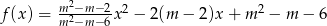 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 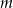 , dla których rozwiązaniem nierówności
, dla których rozwiązaniem nierówności 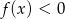 jest przedział postaci
jest przedział postaci 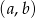 , gdzie
, gdzie 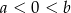 .
.
Rozpatrujemy wszystkie walce, których przekrojem osiowym jest prostokąt, w którym suma długości przekątnej i jednego boku jest równa 10. Oblicz wysokość i promień podstawy tego walca, którego objętość jest największa. Oblicz objętość tego walca.

