/Szkoła średnia/Zadania maturalne/Matura 2016/Matura próbna
Próbny Egzamin Maturalny
z Matematyki (CEN Bydgoszcz)
poziom podstawowy 4 marca 2016 Czas pracy: 170 minut
Zadania zamknięte
Liczba 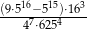 jest równa
jest równa
A)  B)
B) 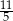 C)
C) 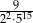 D)
D) 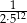
Wyrażenie 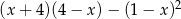 zapisać można w postaci
zapisać można w postaci
A) 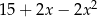 B)
B) 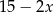 C)
C) 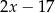 D)
D) 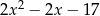
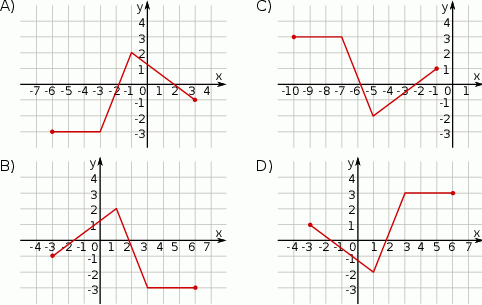
Poniżej przedstawiony jest wykres funkcji 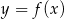 .
.
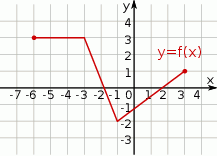
Wskaż wykres funkcji 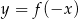 .
.
Ciąg 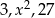 jest ciągiem geometrycznym, gdy
jest ciągiem geometrycznym, gdy
A) tylko 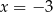 B) tylko
B) tylko 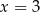 C)
C) 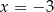 lub
lub 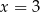 D)
D) 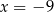 lub
lub 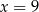
Kąt  jest ostry i
jest ostry i 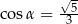 . Wobec tego
. Wobec tego
A) 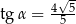 B)
B) 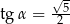 C)
C) 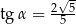 D)
D) 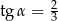
Obwód kwadratu, którego przeciwległe wierzchołki mają współrzędne 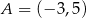 i
i 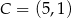 jest równy
jest równy
A) 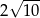 B)
B) 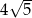 C)
C) 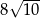 D)
D) 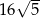
Dane są dwa okręgi styczne wewnętrznie o promieniach 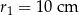 i
i 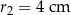 . Zatem odległość między ich środkami jest równa
. Zatem odległość między ich środkami jest równa
A) 2 cm B) 6 cm C) 8 cm D) 14 cm
Rozwiązaniem równania 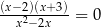 jest
jest
A) 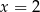 i
i 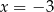 B) tylko
B) tylko 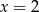 C) tylko
C) tylko 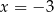 D)
D) 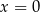 i
i 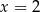
Długość tworzącej stożka jest równa 6, a obwód jego podstawy wynosi 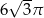 . Kąt rozwarcia tego stożka ma miarę
. Kąt rozwarcia tego stożka ma miarę
A) 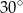 B)
B) 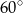 C)
C) 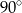 D)
D) 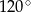
Średnia arytmetyczna zestawu danych: 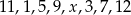 o medianie 7,5 jest równa
o medianie 7,5 jest równa
A) 8 B) 7,5 C) 7 D) 6,75
Suma wyrazów ciągu wyraża się wzorem 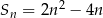 , zatem
, zatem
A) 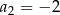 B)
B) 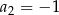 C)
C) 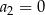 D)
D) 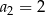
Na rysunku przedstawiono wykres funkcji liniowej 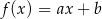 . Zatem
. Zatem
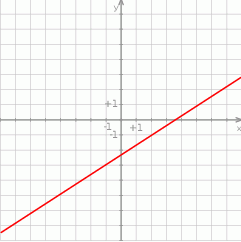
A) 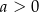 i
i 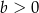 B)
B) 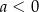 i
i 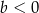 C)
C) 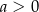 i
i 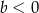 D)
D) 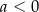 i
i 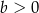
Punkt 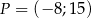 znajduje się na końcowym ramieniu kąta
znajduje się na końcowym ramieniu kąta  . Wówczas
. Wówczas
A) 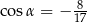 B)
B) 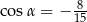 C)
C) 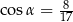 D)
D) 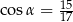
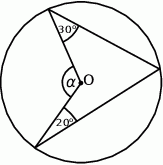
Punkt 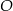 jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy  ma miarę
ma miarę
A) 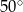 B)
B) 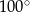 C)
C) 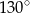 D)
D) 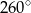
Pole równoległoboku o bokach długości 6 cm i 10 cm i kącie rozwartym o mierze 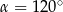 jest równe
jest równe
A) 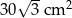 B)
B) 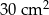 C)
C) 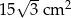 D)
D) 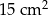
Równanie prostej prostopadłej do prostej 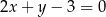 i przechodzącej przez punkt
i przechodzącej przez punkt 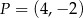 ma postać
ma postać
A) 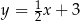 B)
B) 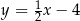 C)
C) 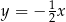 D)
D) 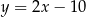
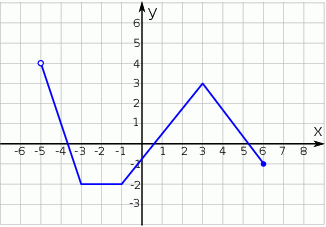
Dany jest wykres funkcji 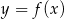 . Dziedziną
. Dziedziną 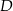 i zbiorem wartości
i zbiorem wartości 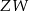 tej funkcji jest
tej funkcji jest
A) 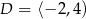 ,
, 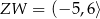 B)
B) 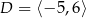 ,
, 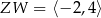
C) 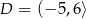 ,
, 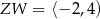 D)
D) 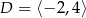 ,
, 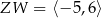
Przekrojem prostopadłościanu zawierającym przekątną podstawy i przekątne sąsiednich ścian bocznych wychodzących z tego samego wierzchołka jest
A) kwadrat B) prostokąt C) trójkąt D) trapez
Ania wyjeżdżając na wakacje zamknęła walizkę za pomocą kodu czterocyfrowego. Pamiętała, że druga liczba jest liczbą pierwszą mniejszą od 7, trzecia jest liczbą nieparzystą, a czwarta to 5, ale zapomniała pierwszej liczby. Ile maksymalnie prób musi wykonać, aby otworzyć walizkę?
A) 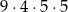 B)
B) 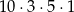 C)
C) 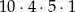 D)
D) 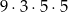
Największa wartość funkcji kwadratowej 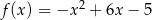 w przedziale
w przedziale 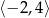 jest równa
jest równa
A) 35 B) 22 C) 4 D) 3
Ilustracją graficzną zbioru rozwiązań nierówności 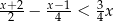 jest przedział
jest przedział
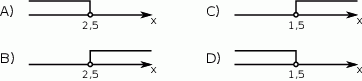
Cena towaru z 22% podatkiem VAT wynosi 183 zł. Cena tego towaru z 7% podatkiem VAT jest równa
A) 160,50 zł B) 195,81 zł C) 210,45 zł D) 223,26 zł
Dany jest fragment wykresu pewnej funkcji kwadratowej 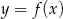 . Funkcja ta ma wzór
. Funkcja ta ma wzór
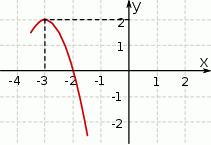
A) 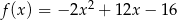 B)
B) 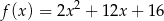
C) 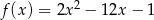 D)
D) 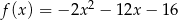
Liczba 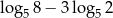 jest równa
jest równa
A) 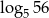 B)
B) 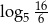 C)
C) 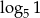 D)
D) 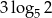
Wzór ogólny ciągu arytmetycznego, w którym 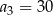 i
i 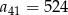 , to
, to
A) 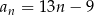 B)
B) 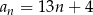 C)
C) 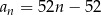 D)
D) 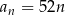
Zadania otwarte
Głośność (w dB) obliczamy ze wzoru 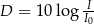 , gdzie
, gdzie 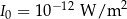 . Oblicz głośność krzyku niemowlencia, dla którego
. Oblicz głośność krzyku niemowlencia, dla którego 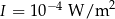 .
.
Ze zbioru liczb 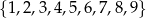 losujemy kolejno bez zwracania trzy liczby, zapisujemy je w kolejności losowania i tworzymy liczbę trzycyfrową w taki sposób, że pierwsza wylosowana liczba jest cyfrą setek, druga jest cyfrą dziesiątek, a trzecia – cyfrą jedności. Oblicz prawdopodobieństwo zdarzenia, że otrzymana liczba trzycyfrowa jest podzielna przez 4. Wynik przedstaw w postaci ułamka nieskracalnego.
losujemy kolejno bez zwracania trzy liczby, zapisujemy je w kolejności losowania i tworzymy liczbę trzycyfrową w taki sposób, że pierwsza wylosowana liczba jest cyfrą setek, druga jest cyfrą dziesiątek, a trzecia – cyfrą jedności. Oblicz prawdopodobieństwo zdarzenia, że otrzymana liczba trzycyfrowa jest podzielna przez 4. Wynik przedstaw w postaci ułamka nieskracalnego.
Dwa okręgi o środkach 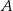 i
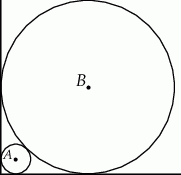
i 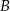 są styczne zewnętrznie i każdy z nich jest jednocześnie styczny do ramion tego samego kąta prostego. Udowodnij, że stosunek obwodu większego z tych okręgów do obwodu mniejszego jest równy
są styczne zewnętrznie i każdy z nich jest jednocześnie styczny do ramion tego samego kąta prostego. Udowodnij, że stosunek obwodu większego z tych okręgów do obwodu mniejszego jest równy 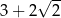 .
.
Rozwiąż nierówność 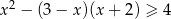 .
.
Oblicz wartość wyrażenia 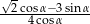 wiedząc, że
wiedząc, że 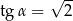 i
i 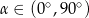 .
.
Liczba naturalna  przy dzieleniu przez 5 daje resztę 3, liczba
przy dzieleniu przez 5 daje resztę 3, liczba 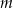 również przy dzieleniu przez 5 resztę 2. Udowodnij, że reszta z dzielenia iloczynu liczb
również przy dzieleniu przez 5 resztę 2. Udowodnij, że reszta z dzielenia iloczynu liczb 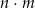 przez 5 daje resztę 1.
przez 5 daje resztę 1.
W ostrosłupie prawidłowym czworokątnym 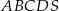 krawędź boczna ma długość 6, a kąt nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa ma miarę
krawędź boczna ma długość 6, a kąt nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa ma miarę 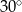 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Ciąg 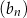 jest arytmetyczny i
jest arytmetyczny i 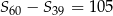 , gdzie
, gdzie 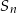 oznacza sumę
oznacza sumę  początkowych wyrazów tego ciągu. Oblicz
początkowych wyrazów tego ciągu. Oblicz  , wiedząc, że liczby
, wiedząc, że liczby 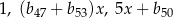 tworzą rosnący ciąg geometryczny.
tworzą rosnący ciąg geometryczny.
Dany jest trójkąt 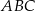 , w którym
, w którym 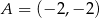 i
i 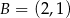 . Wierzchołek
. Wierzchołek 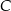 leży na prostej o równaniu
leży na prostej o równaniu 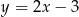 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 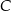 , dla którego suma kwadratów długości boków trójkąta jest najmniejsza.
, dla którego suma kwadratów długości boków trójkąta jest najmniejsza.

