/Szkoła średnia/Zadania maturalne/Matura 2016/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 9 kwietnia 2016 Czas pracy: 180 minut
Zadania zamknięte
Liczba 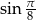 jest równa
jest równa
A) 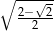 B)
B) 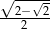 C)
C) 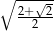 D)
D) 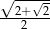
Liczba punktów wspólnych wykresów funkcji 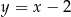 i
i 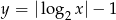 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Liczba 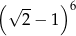 jest równa
jest równa
A) 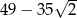 B)
B) 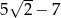 C)
C) 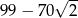 D)
D) 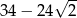
Pochodna funkcji 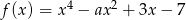 jest funkcją rosnącą jeżeli
jest funkcją rosnącą jeżeli
A) 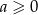 B)
B) 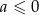 C)
C) 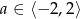 D)
D) 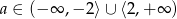
Ile jest liczb naturalnych pięciocyfrowych, których iloczyn cyfr jest dodatnią liczbą złożoną?
A) 59029 B) 59028 C) 89980 D) 89979
Zadania otwarte
Oblicz granicę 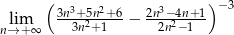 .
.
Długości boków prostokąta są równe 8 oraz 15. Oblicz cosinus kąta rozwartego, który tworzą przekątne tego prostokąta.
Bok  kwadratu
kwadratu  o polu równym 4 jest zawarty w prostej o równaniu
o polu równym 4 jest zawarty w prostej o równaniu 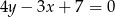 . Wiadomo ponadto, że wewnątrz tego kwadratu leży początek układu współrzędnych. Napisz równanie prostej zawierającej bok
. Wiadomo ponadto, że wewnątrz tego kwadratu leży początek układu współrzędnych. Napisz równanie prostej zawierającej bok 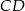 tego kwadratu.
tego kwadratu.
Rozwiąż równanie 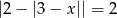 .
.
Czworokąt 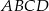 jest wpisany w okrąg oraz pola trójkątów
jest wpisany w okrąg oraz pola trójkątów 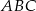 i
i 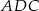 są równe. Wykaż, że
są równe. Wykaż, że
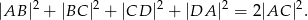
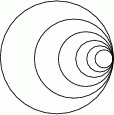
Dane jest koło 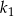 o promieniu
o promieniu  . W tym kole narysowano koło
. W tym kole narysowano koło 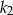 styczne wewnętrznie, którego pole jest równe połowie pola koła
styczne wewnętrznie, którego pole jest równe połowie pola koła 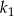 . W kole
. W kole 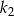 narysowano koło
narysowano koło 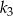 styczne wewnętrznie, którego pole jest równe połowie pola koła
styczne wewnętrznie, którego pole jest równe połowie pola koła 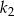 . Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę obwodów wszystkich narysowanych kół.
. Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę obwodów wszystkich narysowanych kół.
Wykaż, że jeżeli 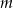 i
i  są takimi liczbami całkowitymi, że rozwiązania równania
są takimi liczbami całkowitymi, że rozwiązania równania 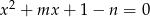 są niezerowymi liczbami całkowitymi, to liczba
są niezerowymi liczbami całkowitymi, to liczba 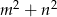 nie jest liczbą pierwszą.
nie jest liczbą pierwszą.
Wykaż, że dla dowolnej liczby rzeczywistej 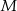 nierówność
nierówność
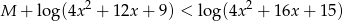
ma przynajmniej jedno rozwiązanie w przedziale 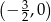 .
.
Rzucamy 5 razy symetryczną monetą. Oblicz prawdopodobieństwo otrzymania co najmniej 4 orłów lub co najmniej 4 reszek, jeżeli wiadomo, że otrzymaliśmy co najmniej jedną reszkę.
Na bokach 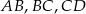 i
i 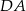 czworokąta
czworokąta 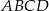 wybrano punkty
wybrano punkty 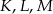 i
i  takie, że
takie, że
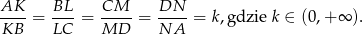
Oblicz stosunek pola czworokąta 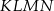 do pola czworokąta
do pola czworokąta 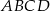 .
.
Podstawą ostrosłupa 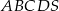 jest kwadrat
jest kwadrat 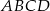 o boku długości
o boku długości  , a krawędź boczna
, a krawędź boczna 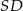 jest wysokością ostrosłupa. Oblicz objętość ostrosłupa jeżeli cosinus kąta między ścianami bocznymi
jest wysokością ostrosłupa. Oblicz objętość ostrosłupa jeżeli cosinus kąta między ścianami bocznymi 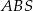 i
i 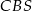 tego ostrosłupa jest równy
tego ostrosłupa jest równy 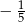 .
.
Ze zbioru 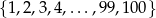 wybieramy cztery różne liczby i obliczamy ich sumę. Oblicz jakie jest prawdopodobieństwo tego, że suma wybranych liczb jest nieparzysta. Wynik podaj w postaci ułamka nieskracalnego.
wybieramy cztery różne liczby i obliczamy ich sumę. Oblicz jakie jest prawdopodobieństwo tego, że suma wybranych liczb jest nieparzysta. Wynik podaj w postaci ułamka nieskracalnego.
Spośród wszystkich trapezów, w których iloczyn długości podstaw jest równy 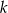 , a pole jest równe
, a pole jest równe 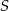 wybrano ten, który ma najdłuższą wysokość. Wykaż, że przekątne wybranego trapezu dzielą się na połowy.
wybrano ten, który ma najdłuższą wysokość. Wykaż, że przekątne wybranego trapezu dzielą się na połowy.

