Zadanie nr 1133773
Ciąg 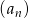 jest geometryczny, a ciąg
jest geometryczny, a ciąg 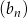 jest arytmetyczny. Pierwszy wyraz
jest arytmetyczny. Pierwszy wyraz 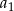 ciągu geometrycznego jest różnicą ciągu arytmetycznego
ciągu geometrycznego jest różnicą ciągu arytmetycznego 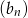 . Wyrazy ciągu
. Wyrazy ciągu 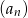 są liczbami całkowitymi, a suma dwóch początkowych wyrazów tego ciągu jest równa 28. Natomiast pierwszy wyraz
są liczbami całkowitymi, a suma dwóch początkowych wyrazów tego ciągu jest równa 28. Natomiast pierwszy wyraz 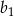 ciągu arytmetycznego jest ilorazem ciągu geometrycznego
ciągu arytmetycznego jest ilorazem ciągu geometrycznego 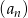 . Suma siedmiu pierwszych wyrazów ciągu arytmetycznego
. Suma siedmiu pierwszych wyrazów ciągu arytmetycznego 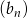 jest równa 126. Wyznacz te ciągi.
jest równa 126. Wyznacz te ciągi.
Rozwiązanie
Spróbujmy zapisać podane informacje
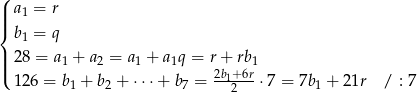
Mamy stąd natychmiast
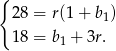
Podstawiamy teraz 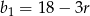 z drugiego równania do pierwszego.
z drugiego równania do pierwszego.
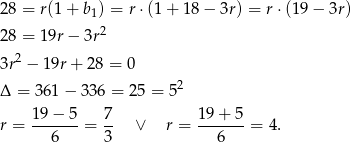
Łatwo sprawdzić, że w pierwszym przypadku nie wszystkie wyrazy ciągu 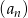 są liczbami całkowitymi, więc musi być
są liczbami całkowitymi, więc musi być 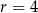 . Wtedy
. Wtedy
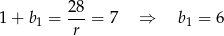
oraz
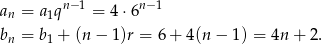
Odpowiedź: 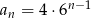 ,
, 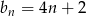 , dla
, dla 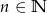 .
.

