/Szkoła średnia/Ciągi

Zadanie nr 1723357

Dodaj do ulubionych
Dodaj do rozwiązanych

Suma 2018 początkowych wyrazów ciągu geometrycznego 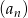(an ) jest równa 1417, a suma odwrotności tych wyrazów jest równa 109. Oblicz iloczyn 2018 początkowych wyrazów ciągu (an) .

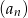Rozwiązanie

Jeżeli zapiszemy 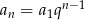n− 1 an = a1q to mamy dane

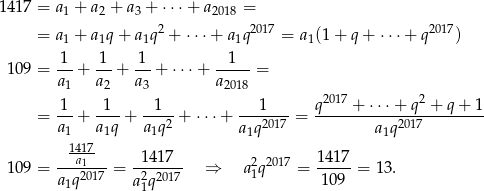
1417 = a + a + a + ⋅⋅⋅+ a = 1 2 3 2018 = a 1 + a1q + a1q2 + ⋅⋅⋅ + a1q2017 = a1(1+ q+ ⋅⋅⋅+ q 2017) 1 1 1 1 109 = --+ ---+ ---+ ⋅ ⋅⋅+ ----- = a1 a2 a3 a2018 1 1 1 1 q2017 + ⋅⋅ ⋅+ q2 + q+ 1 = --+ ----+ ----2 + ⋅⋅⋅+ ---2017-= -----------2017--------- a1 a1q a 1q a1q a1q 1417 141 7 14 17 109 = --a12017-= -2----- ⇒ a21q2017 = ----- = 13 . a1q a1q2017 109

A teraz zobaczmy co mamy obliczyć

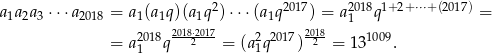
a a a ⋅⋅⋅a = a (a q)(a q2) ⋅⋅⋅(a q2017) = a2018q1+ 2+⋅⋅⋅+(2017) = 1 2 3 2018 1 1 20181⋅2017 1 2018 1 = a21018q--2--- = (a21q2017)-2- = 13 1009.

 
Odpowiedź: 131009

Wersja PDF